HomeEngineeringCivilStructuralMathematicsGeometryPlane GeometrySquare Channel
Print

Square Channel

on . Posted in Plane Geometry

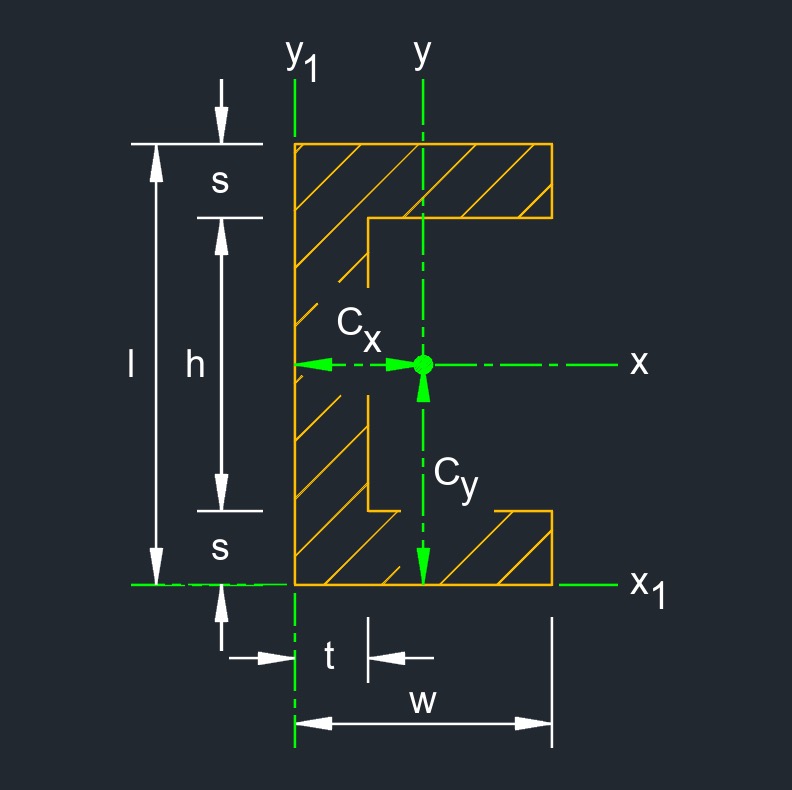C square 1A square channel, also called square C-channel or square U-channel, is a type of structural steel member with a cross-sectional shape resembling the letter "C" or "U."  In the case of a square channel, the cross-sectional shape is square rather than the more common rectangular shape of a standard C-channel or U-channel.  It has four equal length sides forming a square, and one side of the square is open.

Square channels are often used in construction and engineering applications where a combination of torsional resistance, load-bearing capacity, and ease of connection is required.  The open side of the square channel provides a convenient space for attaching other structural components, fasteners, or fixtures.

Square Channel Index

 

area of a Square Channel formula
\(\large{ A =  w\;l - h \; \left( w - t  \right)  }\)
Symbol English Metric
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Distance from Centroid of a Square Channel formulas

\(\large{ C_x =  \frac{ 2\;w^2 \;s \;+\; h\;t^2  }{ 2\;w\;l \;-\; 2\;h \; \left( w \;-\; t  \right)  }  }\)

\(\large{ C_y =  \frac{ l  }{ 2}  }\)
Symbol English Metric
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Elastic Section Modulus of a Square Channel formulas

\(\large{ S_{x} =  \frac{ I_{x} }{ C_{y}   } }\) 

\(\large{ S_{y} =  \frac{ I_{y} }{ C_{x}   } }\) 
Symbol English Metric
\(\large{ S }\) = elastic section modulus \(\large{ in^3 }\) \(\large{ mm^3 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Perimeter of a Square Channel formula
\(\large{ P =  2 \; \left( 2\;w + l \; \right)  - 2\;t  }\) 
Symbol English Metric
\(\large{ P }\) = perimeter \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Polar Moment of Inertia of a Square Channel formulas

\(\large{ J_{z} =  I_{x}  +  I_{y} }\) 

\(\large{ J_{z1} =  I_{x1}  +  I_{y1} }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Radius of Gyration of a Square Channel formulas

\(\large{ k_{x} =  \sqrt {     \frac{ w\;l^3 \;-\; h^3 \; \left( w \;-\; t  \right) }{ 12 \; \left[   w\;l \;-\; h \; \left( w \;-\; t  \right)    \right]  }          }   }\) 

\(\large{ k_{y} =  \sqrt  {  \frac{ I_{y} }{ A  }   }   }\) 

\(\large{ k_{z} =  \sqrt  {  k_{x}{^2} + k_{y}{^2}    }  }\) 

\(\large{ k_{x1} =  \sqrt  {  \frac{ I_{x1} }{ A  }   }   }\)

\(\large{ k_{y1} =  \sqrt  {  \frac{ I_{y1} }{ A  }   }   }\)

\(\large{ k_{z1} =  \sqrt  {  k_{x1}{^2} + k_{y1}{^2}    }  }\)
Symbol English Metric
\(\large{ k }\) = radius of gyration \(\large{ in }\) \(\large{ mm }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Second Moment of Area of a Square Channel formulas

\(\large{ I_{x} =  \frac{ w\;l^3 \;-\; h^3 \; \left( w \;-\; t  \right) }{ 12 }  }\)

\(\large{ I_{y} =  \frac{ 2\;s\;w^3 \;+\; h\;t^3 }{ 3 } - A\;C_{x}{^2} }\) 

\(\large{ I_{x1} =  I_{x}  +  A\;C_{y}{^2} }\) 

\(\large{ I_{y1} =  I_{y}  +  A\;C_{x}{^2} }\)
Symbol English Metric
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Torsional Constant of a Square Channel formula
\(\large{ J  =   \frac{  2 \; \left( w \;-\;  \frac{t}{2}  \right)  \; s^3 \; \left( l \;-\; s  \right) \; t^3  }{  3  }  }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

Tags: Structural Steel

Latest Articles