- See Article - Geometric Properties of Structural Shapes
area of a Square Channel formula |
||
| \( A \;=\; t \cdot \left( 2\cdot w - t \right) \) | ||
| Symbol | English | Metric |
| \( A \) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \( t \) = thickness | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
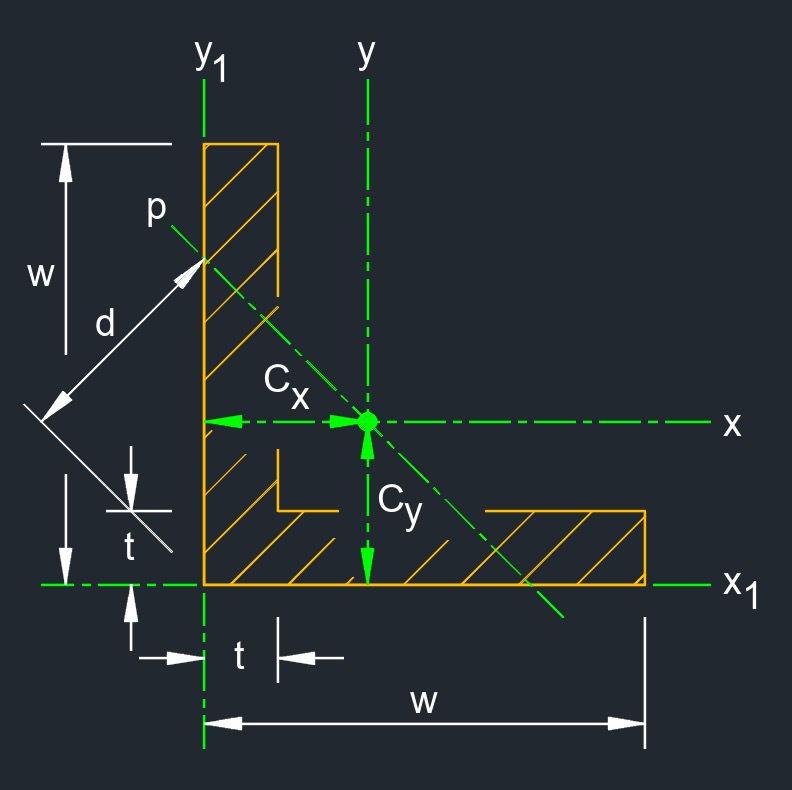Square angle is an angle iron with square legs, creating a right angle. This type of angle iron has equal length sides forming a 90-degree corner. It's commonly used as a structural component in various construction and engineering applications due to its rigidity and load-bearing capacity. Square angles, like other angle iron profiles, come in various sizes, thicknesses, and materials to accommodate different load-bearing capacities and design requirements. The cross-sectional properties of the angle, such as the moment of inertia and section modulus, determine its performance under different loading conditions.
Distance from Centroid of a Square Angle formulas |
||
|
\( C_x \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) } \) \( C_y \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) } \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \(\large{ in }\) | \(\large{ mm }\) |
| \( t \) = thickness | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
Elastic Section Modulus of a Square Angle formulas |
||
|
\( S_x \;=\; \dfrac{ I_x }{ C_y } \) \( S_y \;=\; \dfrac{ I_y }{ C_x } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \(\large{ in^3 }\) | \(\large{ mm^3 }\) |
| \( C \) = distance from centroid | \(\large{ in }\) | \(\large{ mm }\) |
| \( I \) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
Perimeter of a Square Angle formula |
||
| \( P \;=\; 4\cdot w \) | ||
| Symbol | English | Metric |
| \( P \) = perimeter | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
Polar Moment of Inertia of a Square Angle formulas |
||
|
\( J_{z} \;=\; I_{x} + I_{y} \) \( J_{z1} \;=\; I_{x1} + I_{y1} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
| \( I \) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
Principal Axis of a Square Angle formula |
||
| \( d \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) \cdot cos( 45^\circ) } \) | ||
| Symbol | English | Metric |
| \( d \) = distance from principle axis | \(\large{ in }\) | \(\large{ mm }\) |
| \( t \) = thickness | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
Radius of Gyration of a Square Angle formulas |
||
|
\( k_{x} \;=\; \sqrt{ \dfrac { I_{x} }{ A } } \) \( k_{y} \;=\; \sqrt{ \dfrac { I_{y} }{ A } } \) \( k_{z} \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \sqrt{ \dfrac { I_{x1} }{ A } } \) \( k_{y1} \;=\; \sqrt{ \dfrac { I_{y1} }{ A } } \) \( k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \(\large{ in }\) | \(\large{ mm }\) |
| \( A \) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \( I \) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
Second Moment of Area of a Square Angle formulas |
||
|
\( I_{x} \;=\; \dfrac{ t \cdot \left( w - C_y \right)^3 + w \cdot \left[ w - \left( w - C_y \right) \right]^3 - \left( w - t \right) \cdot \left[ w - \left( w - C_y \right) - t \right]^3 }{3} \) \( I_{x} \;=\; \dfrac{ t \cdot \left( w - C_y \right)^3 + w \cdot \left[ w - \left( w - C_y \right) \right]^3 - \left( w - t \right) \cdot \left[ w - \left( w - C_y \right) - t \right]^3 }{3} \) \( I_{x1} \;=\; I_{x} + A\cdot C_{y} \) \( I_{y1} \;=\; I_{y} + A\cdot C_{x} \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
| \( A \) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \( C \) = distance from centroid | \(\large{ in }\) | \(\large{ mm }\) |
| \( t \) = thickness | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
Tortional Constant of a Square Angle formula |
||
| \( J \;=\; \dfrac{ \left[ w - \left( \dfrac {t}{2} \right) \right] + \left[ w - \left( \dfrac {t}{2} \right) \right] \cdot t^3 }{3} \) | ||
| Symbol | English | Metric |
| \( J \) = torsional constant | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
| \( t \) = thickness | \(\large{ in }\) | \(\large{ mm }\) |
| \( w \) = width | \(\large{ in }\) | \(\large{ mm }\) |
