HomeEngineeringCivilStructuralMathematicsGeometryPlane GeometryZed
Print

Zed

on . Posted in Plane Geometry

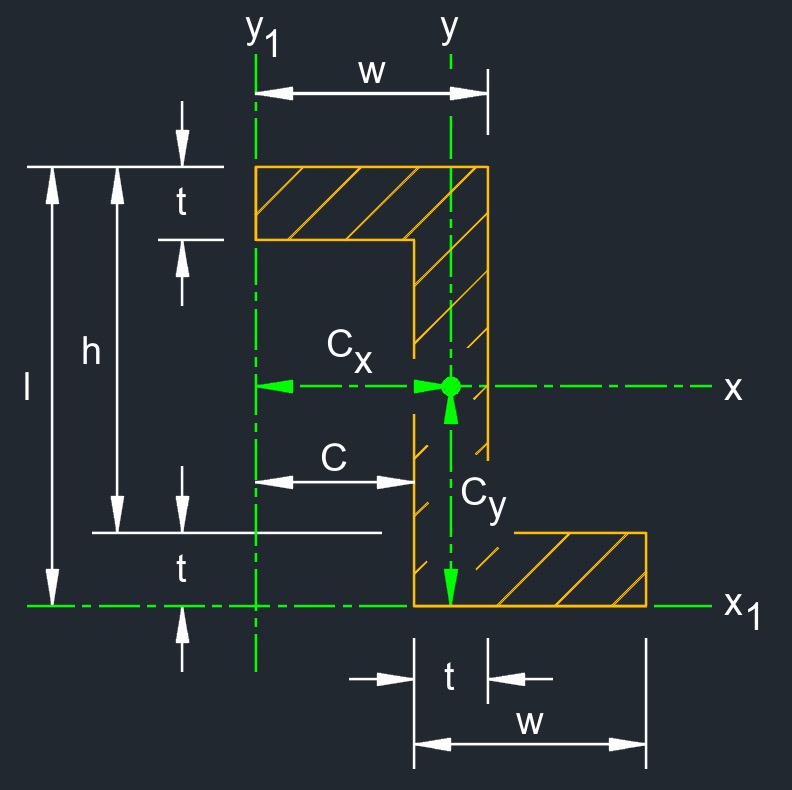Zed beam 1Zed beam, also called known as a "Z-shaped" or "Z-section" beam, is a variation of the letter "Z," which reflects the shape of the cross-sectional profile of the beam.  A Zed beam, or Z-section beam, has a cross-sectional shape resembling the letter "Z," with flanges (horizontal top and bottom parts) that are parallel and connected by a vertical web.  The flanges are usually smaller in width than those of an I-beam, and they extend outward from the web at the top and bottom.  The web connects the two flanges and provides vertical rigidity to the beam.

Zed Index

 

area of a Zed formula
\(\large{ A =   t \; \left[ l  +  2 \;  \left( w - t  \right)  \right]  }\)
Symbol English Metric
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ l }\) = height  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

 

Distance from Centroid of a Zed formulas

\(\large{ C_x =  \frac{ 2\;w \;-\; t }{ 2  }  }\) 

\(\large{ C_y =  \frac{ l }{ 2  }  }\) 
Symbol English Metric
\(\large{ C }\) = distance from centroid  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

 

Elastic Section Modulus of a Zed formulas

\(\large{ S_{x} =  \frac{ I_{x} }{ C_{y}   } }\) 

\(\large{ S_{y} =  \frac{ I_{y} }{ C_{x}   } }\) 
Symbol English Metric
\(\large{ S }\) = elastic section modulus \(\large{ in^3 }\) \(\large{ mm^3 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Perimeter of a Zed formula
\(\large{ P =  2 \; \left( w  +  l \right) - t  }\) 
Symbol English Metric
\(\large{ P }\) = perimeter  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ l }\) = height  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ t }\) = thickness  \(\large{ in }\) \(\large{ mm }\) 
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Polar Moment of Inertia of a Zed formulas

\(\large{ J_{z} =  I_{x}  +  I_{y} }\) 

\(\large{ J_{z1} =  I_{x1}  +  I_{y1} }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Radius of Gyration of a Zed formulas

\(\large{ k_{x} =  \sqrt{  \frac {  w\;l^3 \;-\;  c \; \left( l \;-\; 2\;t \right)^3   }{ 12\;t \; \left[  l \;+\;  2 \; \left( w \;-\; t \right) \right]    }   }   }\) 

\(\large{ k_{y} =    \frac{ l \; \left( w \;+\; c \right)^3 \;-\; 2c^3 \;h  \;-\; 6\;w^2\; c\;h   }{ 12\;t \; \left[  l \;+\;  2 \; \left( w \;-\; t \right) \right]    }    }\) 

\(\large{ k_{z} =    \sqrt{  k_{x}{^2} + k_{y}{^2}  } }\) 

\(\large{ k_{x1} =  \sqrt{  \frac{ I_{x1} }{ A  }   }   }\)

\(\large{ k_{y1} =  \sqrt{  \frac{ I_{y1} }{ A  }   }   }\)

\(\large{ k_{z1} =    \sqrt{  k_{x1}{^2} + k_{y1}{^2}  } }\)
Symbol English Metric
\(\large{ k }\) = radius of gyration \(\large{ in }\) \(\large{ mm }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ c }\) = width \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Second Moment of Area of a Zed formulas

\(\large{ I_{x} =   \frac{  w\;l^3 \;-\;  c \;  \left( l \;-\; 2\;t \right)^3   }{12}   }\) 

\(\large{ I_{y} =   \frac{   l \;  \left( w \;+\; c \right)^3 \;-\; 2\;c^3\; h \;-\; 6\;w^2 \;c\;h   }{12}   }\) 

\(\large{ I_{x1} =  I_{x}  +  A\;C_{y}{^2} }\) 

\(\large{ I_{y1} =  I_{y}  +  A\;C_{x}{^2} }\)
Symbol English Metric
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ c }\) = width \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

Tags: Structural Steel

Latest Articles