- See Article - Geometric Properties of Structural Shapes
Area of a Trapezoid formulas |
||
|
\( A_{area} \;=\; h \cdot \left( \dfrac{ c + a }{ 2 } \right) \) \( A_{area} \;=\; m\cdot h \) |
||
| Symbol | English | Metric |
| \( A_{area} \) = area | \( in^2 \) | \( mm^2 \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( m \) = midline | \( in \) | \( mm \) |
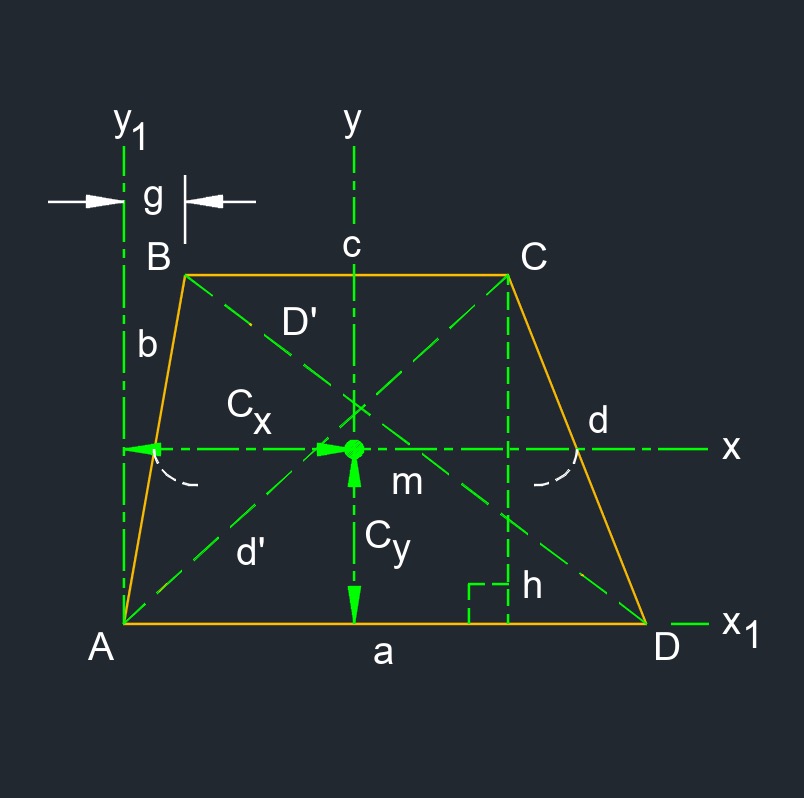Trapezoid (a two-dimensional figure) is a quadrilateral that has a pair of parallel opposite sides.- Acute angle measures less than 90°.
- Diagonal is a line from one vertices to another that is non adjacent.
- No interior angles are equal.
- Obtuse angle measures more than 90°.
- Quadrilateral (a two-dimensional figure) is a polygon with four sides.
Diagonal of a Trapezoid formulas |
||
|
\( d' \;=\; \sqrt{ a^2 + b^2 - 2\cdot a\cdot \sqrt{ b^2 - h^2} } \) \( D' \;=\; \sqrt{ a^2 + d^2 - 2\cdot a\cdot \sqrt{d^2 - h^2} } \) |
||
| Symbol | English | Metric |
| \( d', D' \) = diagonal | \( in \) | \( mm \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
- a & c are bases
- b & d are legs
- a ∥ c
- a ≠ c
- ∠A + ∠B = 180°
- ∠C + ∠D = 180°
- 2 diagonals
- 4 edges
- 4 vertexs
Distance from Centroid of a Trapezoid formulas |
||
|
\( C_x \;=\; \dfrac{ 2\cdot c\cdot g + c^2 + g\cdot a + c\cdot a + a^2 }{ 3 \left( { c + a } \right) } \) \( C_y \;=\; \dfrac{ h }{ 3} \cdot \left( \dfrac{ 2c + a }{c + a} \right) \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( g \) = offset | \( in \) | \( mm \) |
Elastic Section Modulus of a Trapezoid formulas |
||
|
\( S_x \;=\; \dfrac{ I_x }{ C_y } \) \( S_y \;=\; \dfrac{ I_y }{ C_x } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \(lbm \;/\; ft^2-sec\) | \(kg \;/\;m^2\) |
Height of a Trapezoid formulas |
||
|
\( h \;=\; \dfrac{ 2\cdot A_{area} }{c + a} \) \( h \;=\; \dfrac{ A_{area} }{m} \) |
||
| Symbol | English | Metric |
| \( h \) = height | \( in \) | \( mm \) |
| \( A_{area} \) = area | \( in^2 \) | \( mm^2 \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
Midline of a Trapezoid formula |
||
| \( m \;=\; \dfrac{a + c}{2} \) | ||
| Symbol | English | Metric |
| \( m \) = midline | \( in \) | \( mm \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
Perimeter of a Trapezoid formulas |
||
|
\( P \;=\; a + b + c + d \) \( P \;=\; \sqrt {h^2 + g^2} + \sqrt {h^2 + \left( a - c - g \right)^2 } + a + c \) |
||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Plastic Section Modulus of a Trapezoid formulas |
||
|
\( Z_x \;=\; \dfrac{ h^2 \cdot \left( g\cdot c^2 + 14\cdot c\cdot a + g\cdot a^2 \right) }{ 12\cdot \left( c + a \right) } \) \( Z_y \;=\; \dfrac{ 6\cdot c\cdot a\cdot h - 3\cdot c^2\cdot h - 8\cdot c + 8\cdot a + 4\;g^2 \cdot h - 8\cdot g }{ 24} \) |
||
| Symbol | English | Metric |
| \( Z \) = plastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Polar Moment of Inertia of a Trapezoid formulas |
||
|
\( J_{z} \;=\; I_x + I_y \) \( J_{z1} \;=\; I_{x1} + I_{y1} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( I \) = moment of inertia | \(lbm \;/\; ft^2-sec\) | \(kg \;/\; m^2\) |
Radius of Gyration of a Trapezoid formulas |
||
|
\( k_{x} \;=\; \dfrac {h}{6} \cdot \sqrt{ 2 + \dfrac{ 4\cdot c\cdot a}{ \left( c + a \right)^2 } } \) \( k_{y} \;=\; \sqrt { \dfrac {I_y}{A_{area}} } \) \( k_{z} \;=\; \sqrt { k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \dfrac{1}{6} \cdot \sqrt{ \dfrac{ 6\cdot h^2 \cdot \left( 3\cdot c + a \right) }{c + a} } \) \( k_{y1} \;=\; \sqrt { \dfrac {I_{y1}} {A_{area}} } \) \( k_{z1} \;=\; \sqrt { k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Second Moment of Area of a Trapezoid formulas |
||
|
\( I_{x} \;=\; \dfrac{ h^3 \cdot \left( c^2\cdot 4\cdot c\cdot a + a^2 \right) }{ 36 \cdot \left( c + a \right) } \) \( I_{y} \;=\; \dfrac{ h \cdot \left( 4\cdot c\cdot a\cdot g^2 + 3\cdot c^2\cdot a\;g - 3\cdot c\cdot a^2\cdot g + c^4 + a^4 + 2\cdot c^3 \cdot a + c^2 \cdot g^2 + c^3 \cdot g + 2\cdot c\cdot a^3 - g\cdot a^3 + a^2\cdot g^2 \right) } { 36 \cdot \left( c + a \right) } \) \( I_{x1} \;=\; \dfrac{ h^3 \cdot \left( 3\cdot c + a \right) }{12} \) \( I_{y1} \;=\; \dfrac{ h \cdot \left( c^3 + 3\cdot c\cdot g^2 + 3\cdot c^2\cdot g + a^3 + g\cdot a^2 + c\cdot a^2 + a\cdot g^2 + 2\cdot c\cdot a\cdot g + a\cdot c^2 \right) }{12} \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
Edge of a Trapezoid formulas |
||
|
\( a \;=\; 2 \cdot \dfrac { A_{area} }{h} - c \) \( b \;=\; P - c - a - d \) \( c \;=\; 2 \cdot \dfrac {A_{area} }{h} - a \) \( d \;=\; P - c - a - b \) |
||
| Symbol | English | Metric |
| \( a, b, c, d \) = edge | \( in \) | \( mm \) |
| \( A_{area} \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |