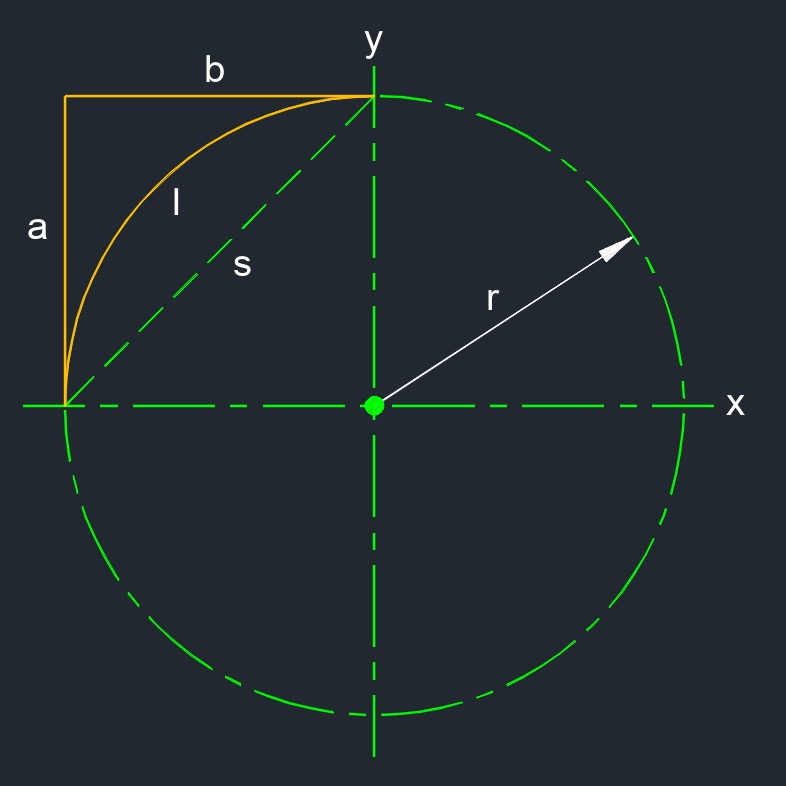
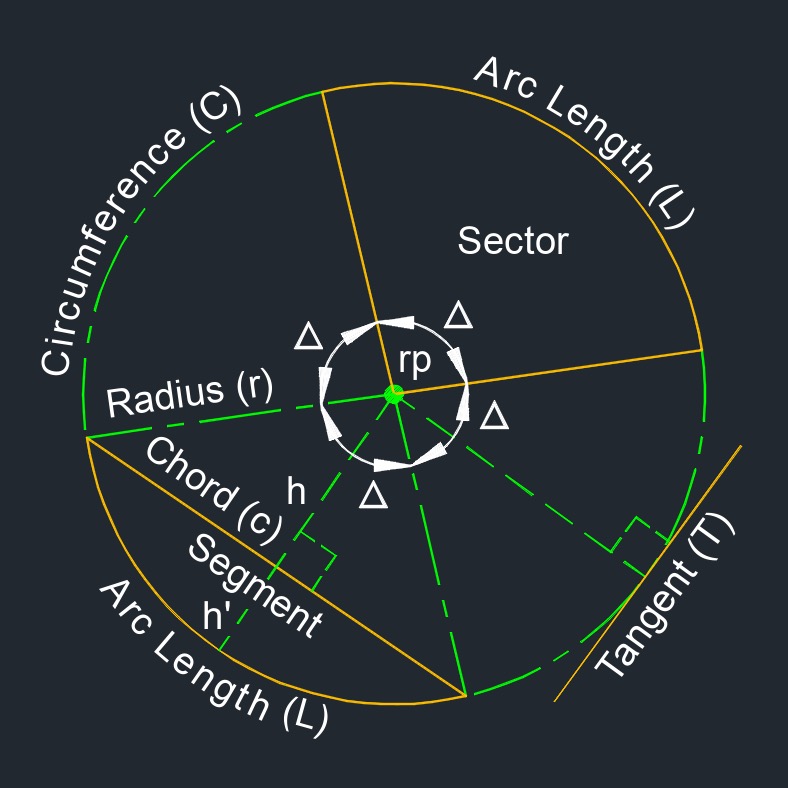
Circle Corner

• Circle corner (a two-dimensional figure) is a right triangle having acute vertices on a circle with the hypotenuse outside the circle.
• Chord is a line segment on the interior of a circle.
• Segment of a circle is an interior part of a circle bound by a chord and an arc.

• Tags: Circle

Circle Corner Index

• Area of a Circle Corner
• Arc Length of a Circle Corner
• Chord Length of a Circle Corner
• Height of a Circle Corner
• Perimeter of a Circle Corner
• Segment Angle of a Circle Corner

 

area of a Circle Corner formula
\( A \;=\; a\;b - r \; L + c \; (r - h)  \;/\;2 \)
Symbol	English	Metric
\( A \) = area	\(ft^2\)	\(m^2\)
\( L \) = arc length	\(ft\)	\(m\)
\( c \) = chord length	\(ft\)	\(m\)
\( a, b \) = edge	\(ft\)	\(m\)
\( r \) = radius	\(ft\)	\(m\)
\( h \) = segment height	\(ft\)	\(m\)

 

Arc Length of a Circle Corner formula
\( L \;=\; r \; \Delta \)
Symbol	English	Metric
\( L \) = arc length	\(ft\)	\(m\)
\( \Delta \) = angle	\(deg\)	\(rad\)
\( r \) = radius	\(ft\)	\(m\)

 

Chord Length of a Circle Corner formula
\( c \;=\; a^2 \; b^2 \)
Symbol	English	Metric
\( c \) = chord length	\(ft\)	\(m\)
\( a, b \) = edge	\(ft\)	\(m\)

 

Height of a Circle Corner formula
\( h \;=\; r \; [\; 1 - cos ( \frac{\Delta}{2} ) \;]   \)
Symbol	English	Metric
\( h \) = segment height	\(ft\)	\(m\)
\( \Delta \) = segment angle	\(deg\)	\(rad\)
\( r \) = radius	\(ft\)	\(m\)

 

Perimeter of a Circle Corner formula
\( p \;=\; a + b + L \)
Symbol	English	Metric
\( p \) = perimeter	\(ft\)	\(m\)
\( L \) = arc length	\(ft\)	\(m\)
\( a, b \) = edge	\(ft\)	\(m\)

 

Segment Angle of a Circle Corner formula
\( \Delta \;=\;   arccos ( 2\;r^2 - c^2 \;/\;2\;r^2)\)
Symbol	English	Metric
\( \Delta \) = segment angle	\(deg\)	\(rad\)
\( c \) = chord length	\(ft\)	\(m\)
\( r \) = radius	\(ft\)	\(m\)