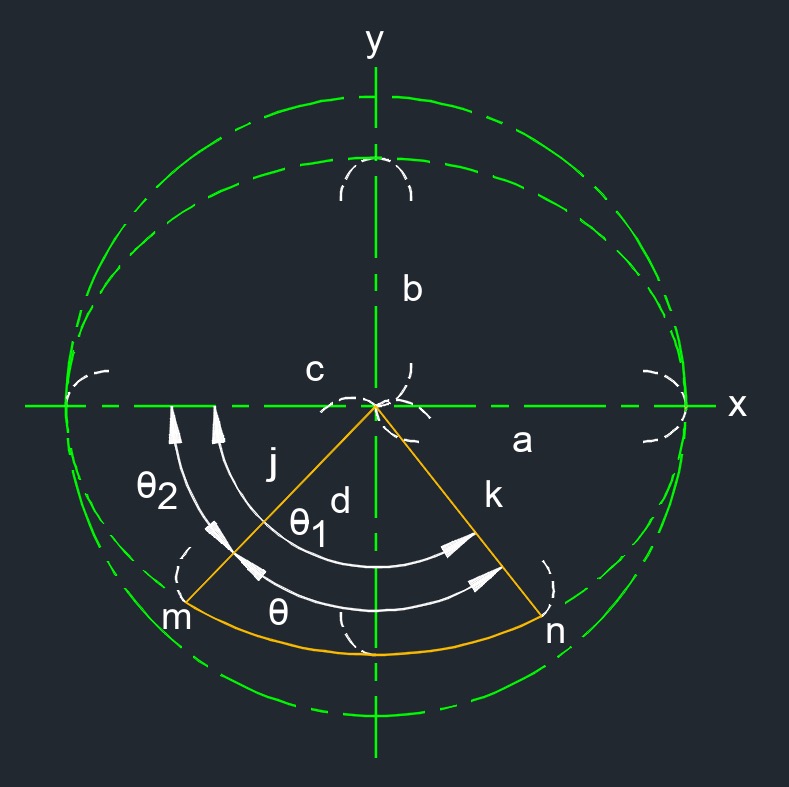
Sector of an Ellipse
Area Sector of an Ellipse formula |
||
| \( A_{area} \;=\; \dfrac{a \cdot b}{2} \cdot \left( {\theta - atan\left[ \dfrac{ a - b \cdot sin(2\cdot \theta_1) }{ a + b + \left(a - b\right) \cdot cos(2\cdot \theta_2) } \right] + atan\left[ \dfrac{ a - b \cdot sin(2\cdot \theta_1) }{ a + b + \left(a - b\right) \cdot cos(2\cdot \theta_2) } \right] } \right) \) | ||
| Symbol | English | Metric |
| \( A_{area} \) = area | \( in^2 \) | \( mm^2 \) |
| \( \theta \) = angle | \( deg\) | \( rad \) |
| \( \theta_1 \) = angle | \( deg \) | \( rad \) |
| \( \theta_2 \) = angle | \( deg \) | \( rad \) |
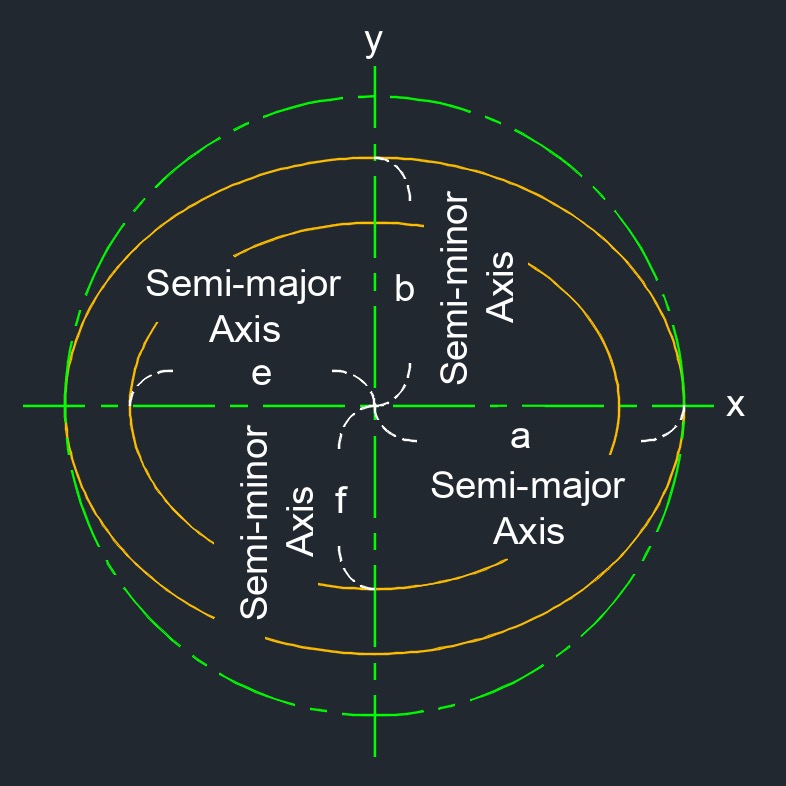
| \( a \) = semi-major axis | \( in \) | \( mm \) |
| \( b \) = semi-minor axis | \( in \) | \( mm \) |
- Ellipse sector (a two-dimensional figure) is a part of the interior of an ellipse having two radius boundries and an arc.
- Sector is a fraction of the area of a ellipse with a radius on each side and an edge.
- Major axis is always the longest axis in an ellipse.
- Minor axis is always the shortest axis in an ellipse.
- Semi-major axis is half of the longest axis of an ellipse.
- Semi-minor axis is half of the shortest axis of an ellipse
Radius Sector of an Ellipse formula |
||
|
\( j \;=\; \sqrt{ \dfrac{ a^2\cdot b^2 }{ a^2\cdot sin^2 (\theta_1) + b^2\cdot cos^2 (\theta_2 ) } } \) \( k \;=\; \sqrt{ \dfrac{ a^2\cdot b^2 }{ a^2\cdot sin^2 (\theta_2) + b^2\cdot cos^2 (\theta_1) } }\) |
||
| Symbol | cdotEnglish | Metric |
| \( j \) = radius | \( in \) | \( mm \) |
| \( k \) = radius | \( in \) | \( mm \) |
| \( \theta_1 \) = angle | \( deg \) | \( rad \) |
| \( \theta_2 \) = angle | \( deg \) | \( rad \) |
| \( a \) = semi-major axis | \( in \) | \( mm \) |
| \( b \) = semi-minor axis | \( in \) | \( mm \) |