Self-intersecting Rectangle
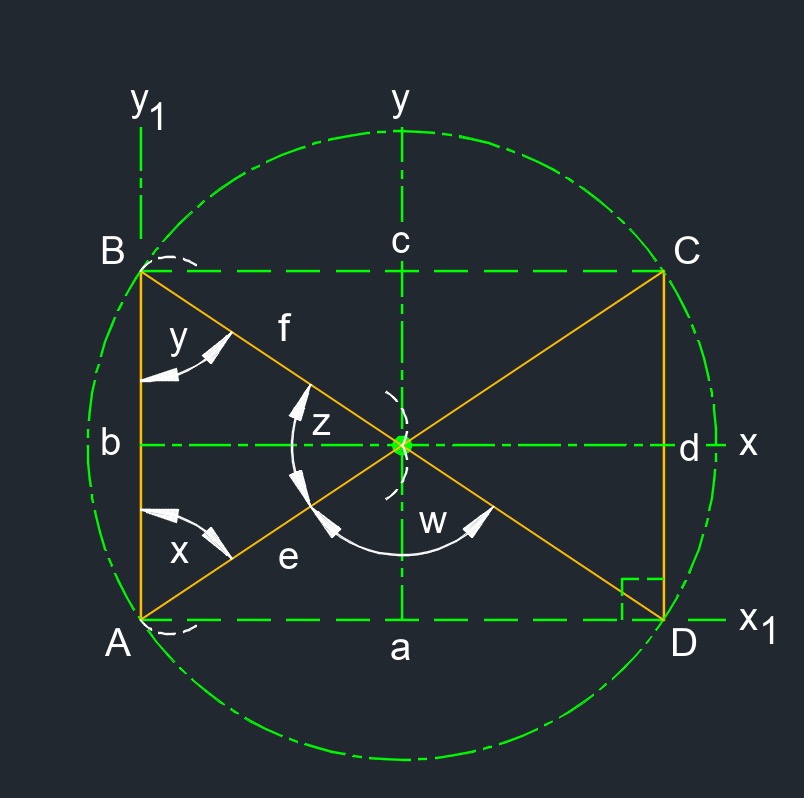Self-intersecting rectangle (a two-dimensional figure) is where one edge crosses over another.- Acute angle measures less than 90°.
- Obtuse angle measures more than 90°.
- x, y, z < 90°
- w > 90°
- b ∥ d
- a = c
- b = d
- e = f
- ∠A = ∠B = ∠C = ∠D
- ∠z + ∠w = 180°
- ∠x + ∠y + ∠z = 180°
- 4 edges
- 4 vertexs
Self-intersecting Rectangle Index
- Area of a Self-intersecting Rectangle
- Angle of a Self-intersecting Rectangle
- Edge of a Self-intersecting Rectangle
- Perimeter of a Self-intersecting Rectangle
Area of a Self-intersecting Rectangle formula |
||
| \(\large{ A_{area} = \frac{a \;b}{2} }\) | ||
| Symbol | English | Metric |
| \(\large{ A_{area} }\) = area | \(\large{ in^2}\) | \(\large{ mm^2}\) |
| \(\large{ b, e }\) = edge | \(\large{ in}\) | \(\large{ mm }\) |
Angle of a Self-intersecting Rectangle formulas |
||
|
\(\large{ x = \frac{180° \;-\; z}{2} }\) \(\large{ z = arccos \left( \frac{2\;e^2 \;-\; b^2}{2\;e^2} \right) }\) \( \large{ w = 180° - z }\) |
||
| Symbol | English | Metric |
| \(\large{ x, y, z }\) = angle | \(\large{ deg}\) | \(\large{ rad}\) |
| \(\large{ w }\) = intersection angle | \(\large{ in}\) | \(\large{ mm }\) |
| \(\large{ b, e }\) = edge | \(\large{ in}\) | \(\large{ mm }\) |
Edge of a Self-intersecting Rectangle formula |
||
| \(\large{ e = \frac{ \sqrt {a^2 \;+\; b^2} }{2} }\) | ||
| Symbol | English | Metric |
| \(\large{ e }\) = edge | \(\large{ in}\) | \(\large{ mm }\) |
| \(\large{ a, b }\) = edge | \(\large{ in}\) | \(\large{ mm }\) |
Perimeter of a Self-intersecting Rectangle formula |
||
| \(\large{ p = 2\; b + 4 \;e }\) | ||
| Symbol | English | Metric |
| \(\large{ p }\) = perimeter | \(\large{ in}\) | \(\large{ mm }\) |
| \(\large{ b, e }\) = edge | \(\large{ in}\) | \(\large{ mm }\) |
Tags: Quadrilateral