Distance from Centroid of a Circle formulas |
||
|
\( C_x \;=\; r \) \( C_y \;=\; r \) \( d \;=\; \sqrt{ ( x - h )^2 + ( y - k )^2 }\) |
||
| Symbol | English | Metric |
| \( C_x, C_y \) = distance from centroid | \( in \) | \( mm \) |
| \( r \) = radius | \( in \) | \( mm \) |
Distance from the centroid of a circle is the distance between the centroid (the geometric center) of the circle and a given point, either inside, on, or outside the circle. The centroid of a circle is simply its center, as a circle is a perfectly symmetric shape, and its centroid coincides with the point at the center of the circle.
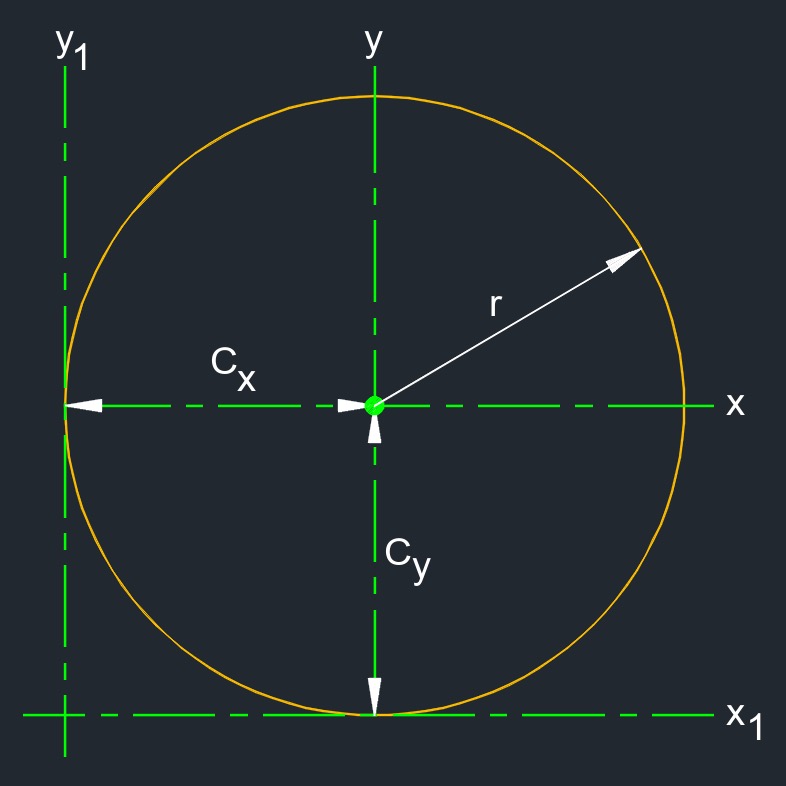
For a circle with center at coordinates (h, k) in a 2D plane, the centroid is at (h, k). The distance from the centroid to any point (x, y) is calculated using the Euclidean distance formula.
