Radius of a Circle

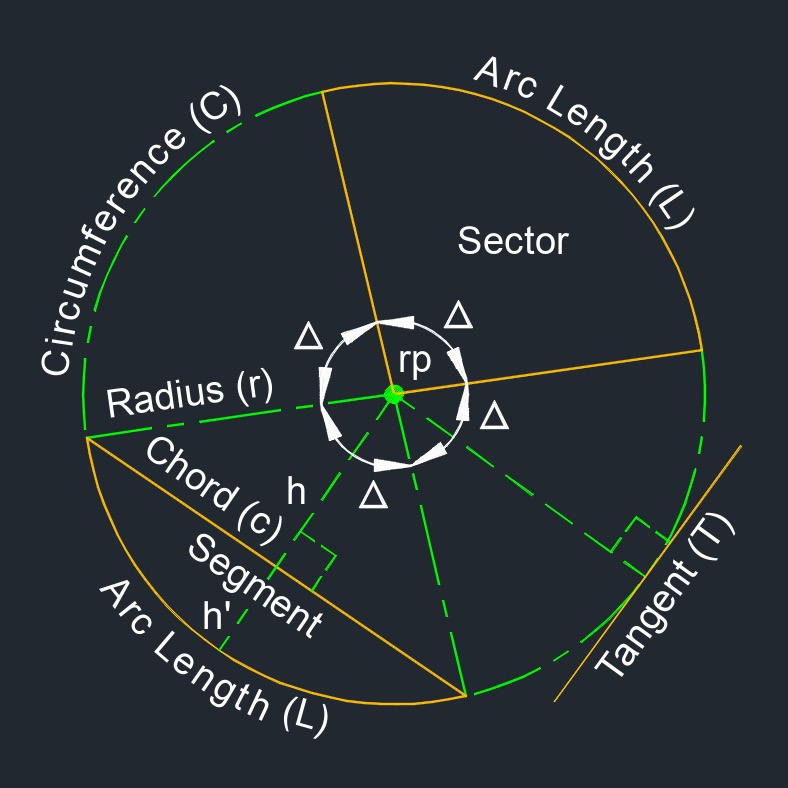Radius, abbreviated as r, of a circle is a fundamental geometric property that defines the distance between the center of the circle and any point on its circumference.  It is a line segment between the center point and a point on a circle or sphere.

Radius is used in many practical applications, ranging from mathematics and geometry to engineering, physics, and everyday life.  It helps define and calculate various aspects of circles, including their size, shape, and proportions.

 

Radius of a Circle formula
\( r \;=\; C\;/\;2 \; \pi \)
Symbol	English	Metric
\( r \) = radius	\( in \)	\(mm \)
\( C \) = circumference	\( in \)	\(mm \)
\( \pi \) = Pi	\(3.141 592 653 ...\)