Mathematics
Mathematics is a discipline that deals with the study of numbers, quantities, and shapes. It involves using logical reasoning and critical thinking to solve problems and develop theories. Mathematics can be divided into many different areas, including algebra, arithmetic, calculus, geometry, statistics, trigonometry, and number theory. 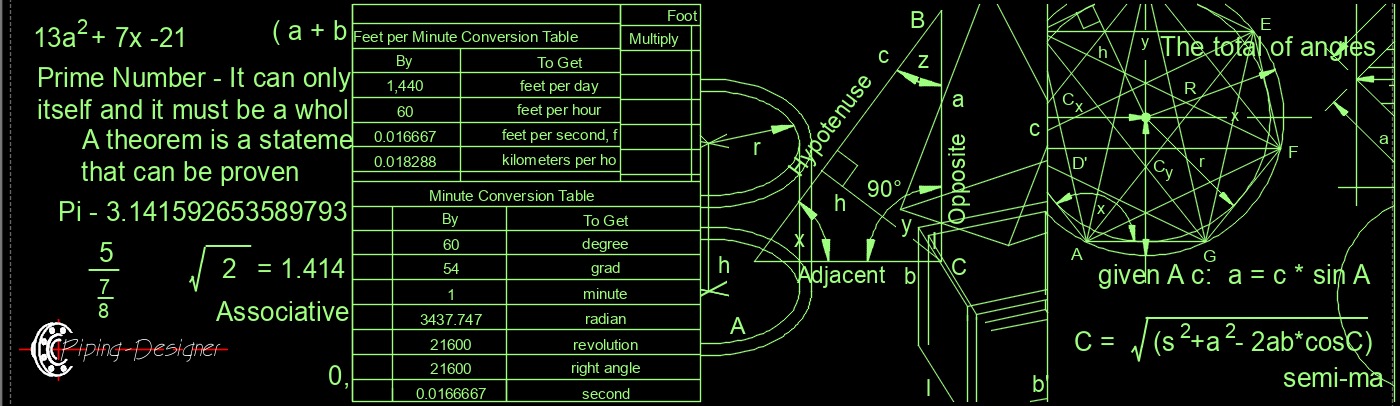Each of these areas has its own concepts and techniques, and they can be applied in a wide range of fields, from physics and engineering to economics and computer science.Mathematics plays a fundamental role in many aspects of modern society, from finance and business to medicine and technology. It provides the tools and techniques needed to analyze and understand complex systems, and to develop solutions to real-world problems.
Mathematics is also a highly abstract and creative field, with a rich history of exploration and discovery. Mathematicians are constantly pushing the boundaries of knowledge, developing new theories and concepts that deepen our understanding of the natural world. Overall, mathematics is a fascinating and essential discipline that plays a critical role in advancing our understanding of the world and in developing new technologies that improve our lives. It is a field that requires curiosity, creativity, and analytical thinking, and it offers endless opportunities for exploration and discovery.
- See Articles - List of Tags, List of Categories, List of Articles, List of Glossaries, Nomenclature and Symbols, (See Mathematics Glossary)
Major Branches of Mathematics
- Applied Mathematics - Applies programs that typically involve a wider range of study to problems that arise in various areas.
- Pure Mathematics - The study of mathematical concepts independently of any application outside matnematics.
- Foundations Mathematics - The study of philosophical and logical.
Science Branches |
||
| Science | ||
| Formal Science | ||
| Mathematics | ||
| Applied Mathematics | Pure Mathematics | Foundation Mathematics |
|
|
|
Tags: Mathematics Glossary