- All edges are the same length
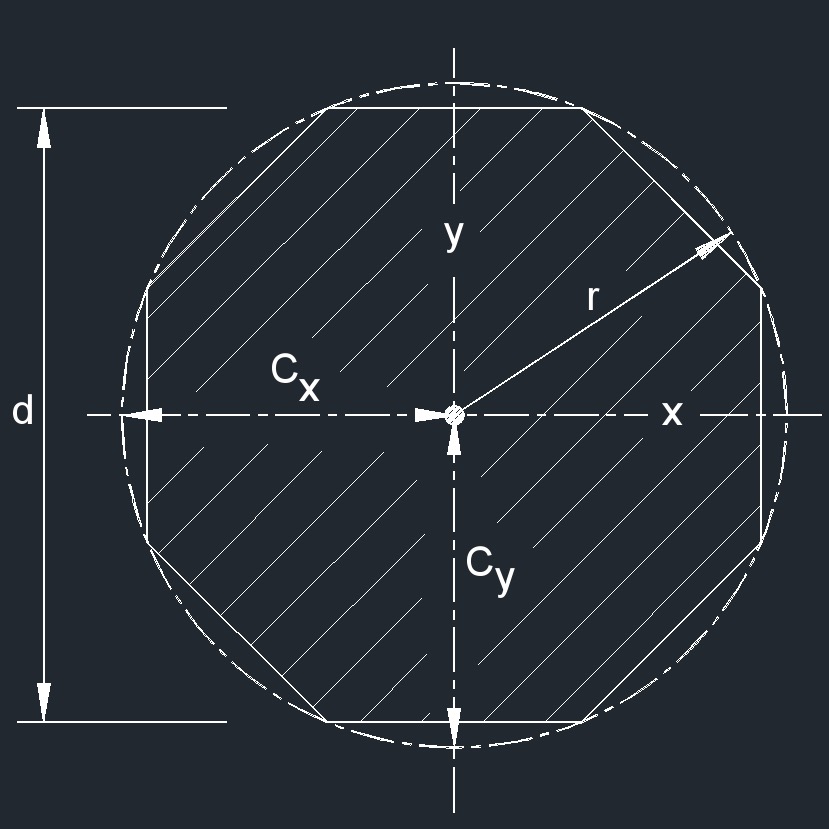
- Interior angles are 135°
- Exterior angles are 45°
- 20 diagonals
- 8 edges
- 8 vertexs
Edge formula
\(a = \sqrt { {\sqrt 2} \frac {A}{2} - \frac {A}{2} } \)
\(a = \frac {p}{8} \)
Where:
\(a\) = edge
\(A\) = area
\(p\) = perimeter
Perimeter formula
\(p= 8a \)
Where:
\(p\) = perimeter
\(a\) = edge
Area formula
\(A = 2 \left( 1 + \sqrt {2} \right) a^2 \)
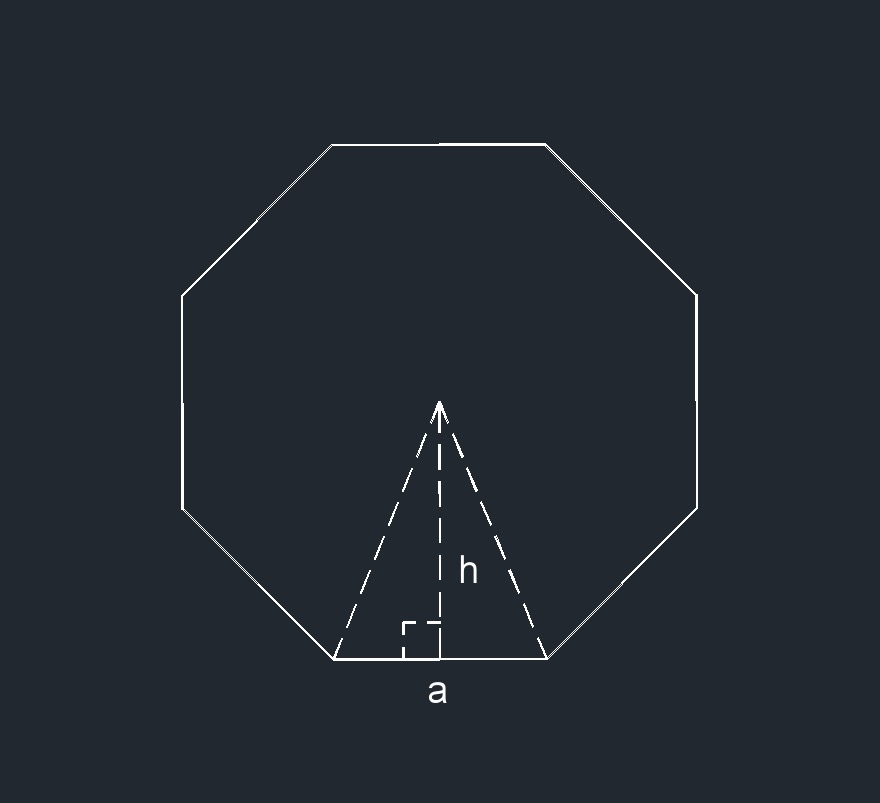
\(A = 8 \left( \frac {1} {2} ah \right) \)
\(A = \frac { a^2 N } { 4 \tan \left( \frac {180°} {N} \right) } \)
\(A = \frac { Ac^2 N \sin \left( \frac {360°} {N} \right) } {2} \)
\(A = Ai^2 N \tan \left( \frac {180°} {N} \right) \)
Where:
\(A\) = area
\(a\) = edge
\(Ac\) = apothem circumcircle (outside radius)
\(Ai\) = apothem incircle (inside radius)
\(N\) = number of edges
\(\sin\) = sine
\(\tan\) = tangent


