- Home
- Science
- Mathematics
- Physics
- Engineering
- Datasheets
- Accessory Datasheets
- Fastener Datasheets
- Fitting Datasheets
- Flange Datasheets
- Blind Flange Datasheets
- Ductile Iron Flange Datasheets
- Expander Flange Datasheets
- Flange Bolt Datasheets
- Lap Joint Flange Datasheets
- Orifice Flange Datasheets
- Slip-On Flange Datasheets
- Socket Flange Datasheets
- Standard Connection Flange Datasheets
- Studding Outlet Flange Datasheets
- Threaded Flange Datasheets
- Weld Neck Flange Datasheets
- Gasket Datasheets
- Pipe & Tubing Dimensions
- Piping Layout Information
- Valve Datasheets
- Standards
- Store
- The World

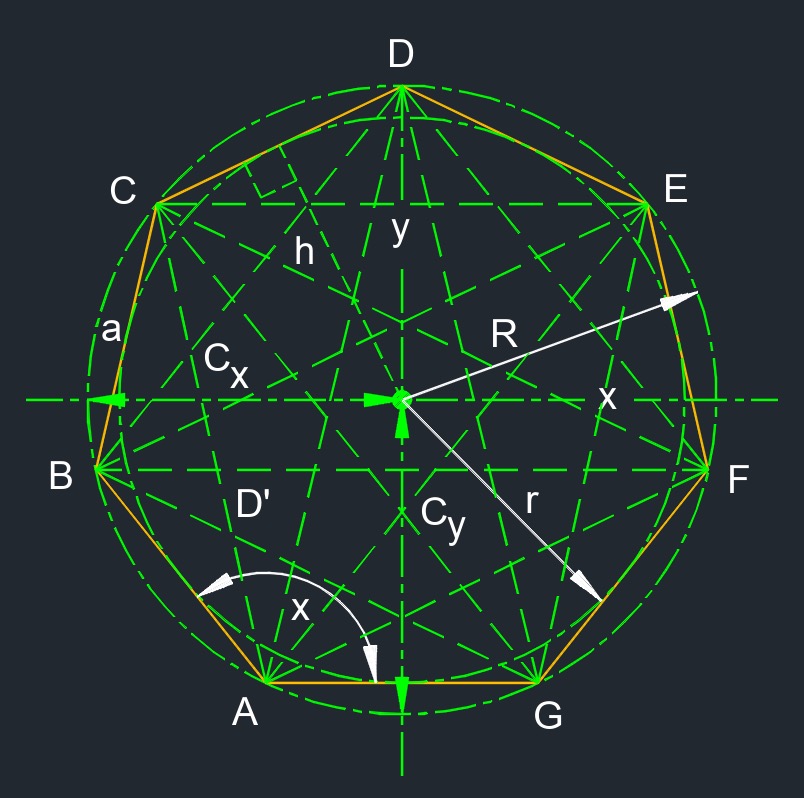 Regular heptagon (a two-dimensional figure) is a polygon with seven congruent sides.
Regular heptagon (a two-dimensional figure) is a polygon with seven congruent sides.