Isosceles Triangle

on 29 January 2016. Posted in Plane Geometry

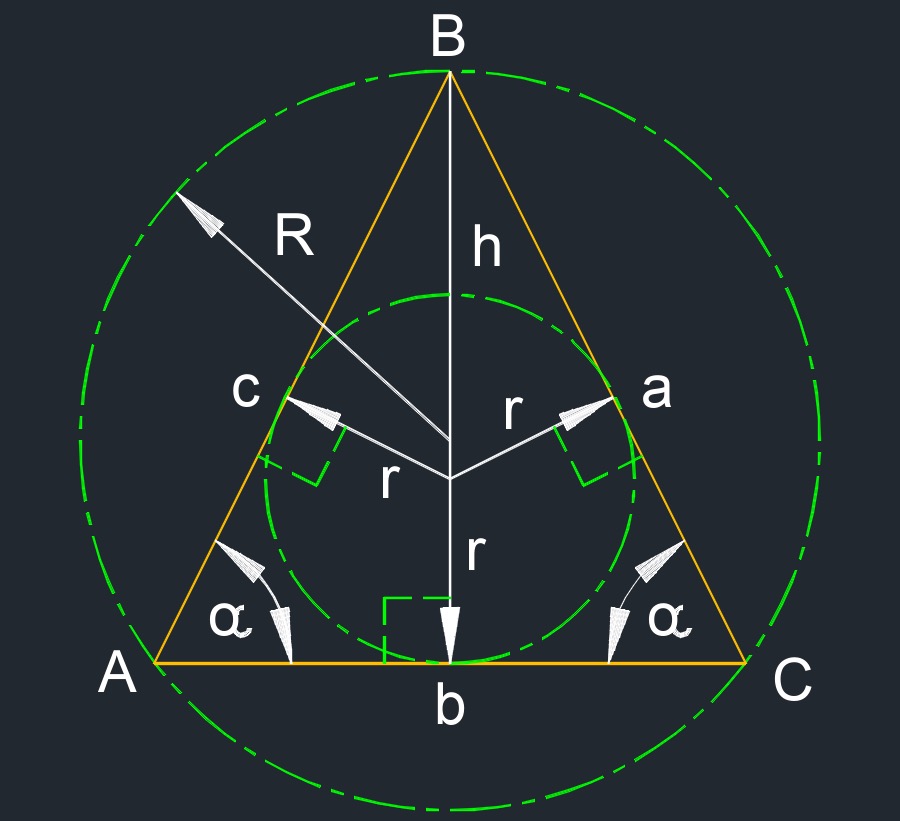
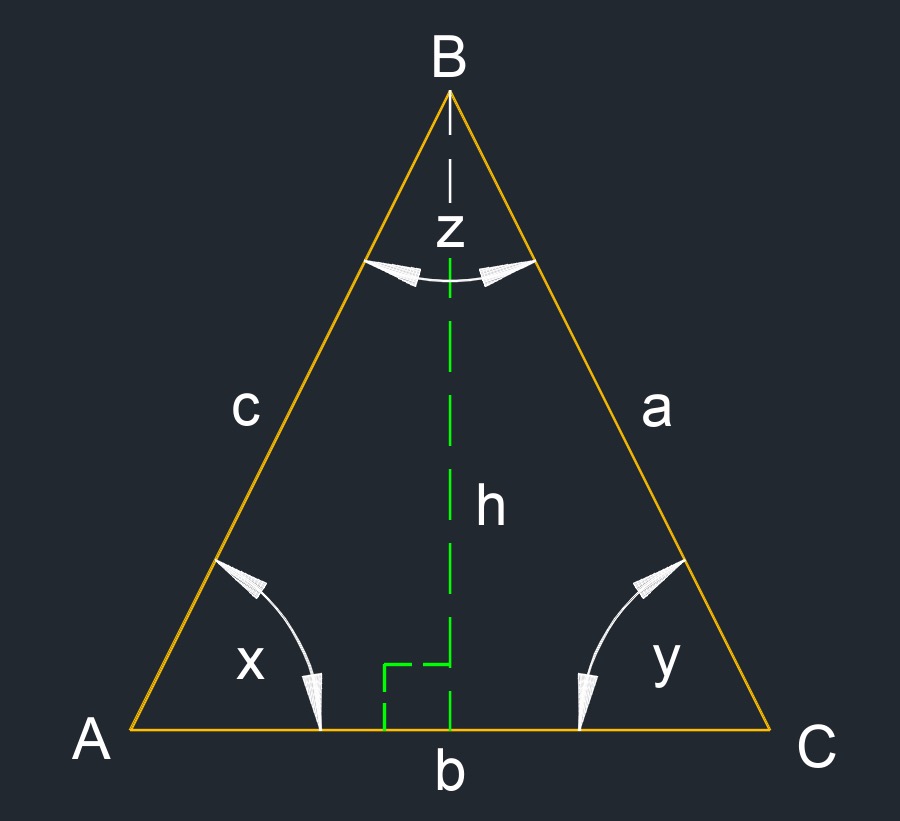Isosceles triangle (a two-dimensional figure) has two sides that are the same length or at least two congruent sides.
Isosceles triangle (a two-dimensional figure) has two sides that are the same length or at least two congruent sides.
Angle bisector of a right isosceles triangle is a line that splits an angle into two equal angles.
Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
Congruent is all sides having the same lengths and angles measure the same.
Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
Semiperimeter is one half of the perimeter.
a = c
x = y
x + y + z = 180°
Height: \(h_a\), \(h_b\), \(h_c\)
Median: \(m_a\), \(m_b\), \(m_c\) - A line segment from a vertex (corner point) to the midpoint of the opposite side
Angle bisectors: \(t_a\), \(t_b\), \(t_c\) - A line that splits an angle into two equal angles
3 edges
3 vertexs

Area of an Isosceles Triangle formula
\(\large{ A_{area} = \frac {h\;b} {2} }\)
Symbol	English	Metric
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ h }\) = height	\(\large{ in }\)	\(\large{ mm }\)

Circumcircle of an Isosceles Triangle formula
\(\large{ R = \frac { a^2 } { \sqrt { 4\; a^2 \;-\; b^2 } } }\)
Symbol	English	Metric
\(\large{ R }\) = outcircle	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ h }\) = height	\(\large{ in }\)	\(\large{ mm }\)

Height of an Isosceles Triangle formula
\(\large{ h = 2 \frac {A_{area}}{b} }\) \(\large{ h = \sqrt { a^2 - \frac {b^2}{4} } }\)
Symbol	English	Metric
\(\large{ h }\) = height	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)

Inscribed Circle of an Isosceles Triangle formulas
\(\large{ r = \frac { b } { 2 } \; \sqrt { \frac { 2\;a \;-\; b } { 2\;a \;+\; b } } }\) (The radius of a inscribed circle (inner) of an Isosceles triangle if given side \(( r )\)) \(\large{ r = a \; \frac { sine \; \alpha \;x\; cos \; \alpha } { 1 \;+\; cos \; \alpha } = \alpha \; cos \; \alpha \;\;x\;\; tan \frac { \alpha } { 2 } }\) (The radius of a inscribed circle (inner) of an Isosceles triangle if given side and angle \(( r )\)) \(\large{ r = \frac {b}{2} \;x\; \frac { sine \; \alpha } { 1 \;+\; cos \; \alpha } = \frac {b}{2} \;x\; tan \frac { \alpha } { 2 } }\) (The radius of a inscribed circle (inner) of an Isosceles triangle if given side and angle \(( r )\)) \(\large{ r = \frac { b\;h } { b \;+\; \sqrt { 4\;h^2 \;+\; b^2 } } }\) (The radius of a inscribed circle (inner) of an Isosceles triangle if given side and height \(( r ) \)) \(\large{ r = \frac { h\; \sqrt { a^2 \;-\; h^2 } } { a \;+\; \sqrt { a^2 \;-\; h^2 } } }\) (The radius of a inscribed circle (inner) of an Isosceles triangle if given side and height \(( r ) \))
Symbol	English	Metric
\(\large{ r }\) = incircle	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ \alpha }\) (Greek symbol alpha) = angle	\(\large{ deg }\)	\(\large{ rad }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ h }\) = height	\(\large{ in }\)	\(\large{ mm }\)

Perimeter of an Isosceles Triangle formula
\(\large{ P = 2\;a + b }\)
Symbol	English	Metric
\(\large{ P }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)

Semiperimeter of an Isosceles Triangle formula
\(\large{ s = \frac{ a \;+\; b \;+\; c }{ 2 } }\)
Symbol	English	Metric
\(\large{ s }\) = semiperimeter	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)

Side of an Isosceles Triangle formulas
\(\large{ a = \frac{P}{2} - \frac{b}{2} }\) \(\large{ b = P - 2\;a }\) \(\large{ b = 2\; \frac{A_{area} }{h} }\)
Symbol	English	Metric
\(\large{ a, b, c }\) = side	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ h }\) = height	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ P }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)

Trig Functions
Find A given a c : \(\; sin \; A= a \div c \) given b c : \(\; cos \; A= b \div c \) given a b : \(\; tan \; A= a \div b \)
Find B given a c : \(\; sin \; B= a \div c \) given b c : \(\; cos \; B= b \div c \) given a b : \(\; tan \; B= b \div a \)
Find a given A c : \(\; a= csin \; A \) given A b : \(\; a= btan \; A \)
Find b given A c : \(\; b= c*cos \; A \) given A a : \(\; b= a \div tan \; A \)
Find c given A a : \(\; c= a \div sin \; A \) given A b : \(\; c= b \div cos \; A \) given a b : \(\; c= \sqrt { a^2+b^2 } \)
Find Area given a b : \(\; Area= a\;b \div 2 \)

Piping Designer Logo 1

Area of an Isosceles Triangle formula