Inside Volume of a Right Hollow cylinder formula |
||
| \( V \;=\; \pi \cdot r^2 \cdot h \) | ||
| Symbol | English | Metric |
| \( V \) = volume (inside) | \( in^3 \) | \(mm^3 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = inside radius | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
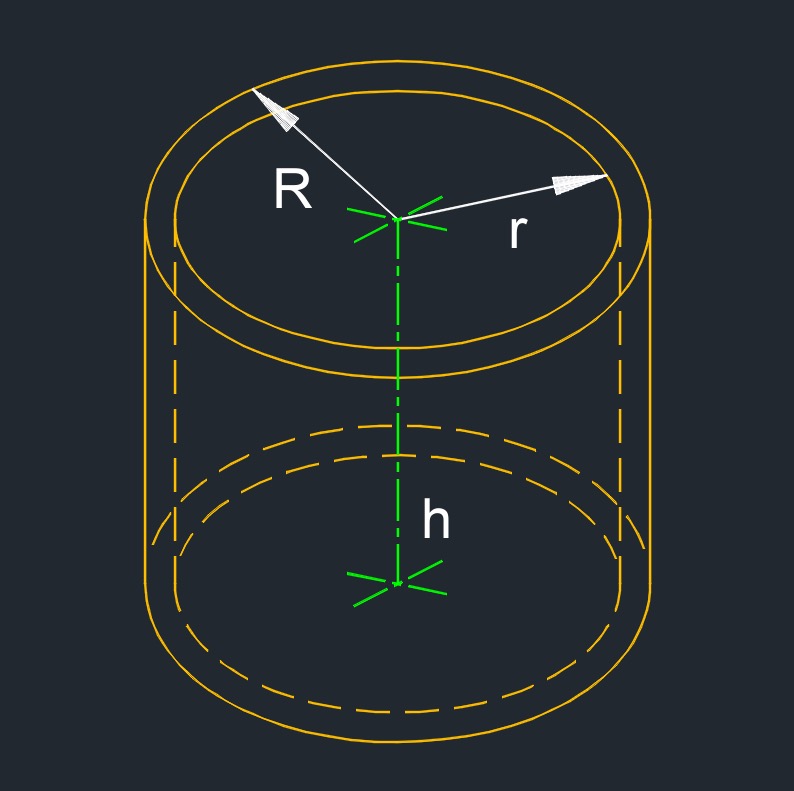Right hollow cylinder (a three-dimensional figure) has a hollow core with both bases direictly above each other and having the center at 90° to each others base.- 2 bases
- Tags: Cylinder
Lateral Surface Area of a Right Hollow cylinder formula |
||
| \( A_l \;=\; 2 \cdot \pi \cdot h \cdot (R^2 + r^2 ) \) | ||
| Symbol | English | Metric |
| \( A_l \) = lateral surface area (side) | \( in^2 \) | \( mm^2 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( h \) = height | \( in \) | \( mm \) |
| \( R \) = outside radius | \( in \) | \( mm \) |
| \( r \) = inside radius | \( in \) | \( mm \) |
Object Volume of a Right Hollow cylinder formula |
||
| \( V \;=\; \pi \cdot h \cdot (R^2 - r^2 ) \) | ||
| Symbol | English | Metric |
| \( V \) = volume (object thickness) | \( in^3 \) | \(mm^3 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( R \) = outside radius | \( in \) | \( mm \) |
| \( r \) = inside radius | \( in \) | \( mm \) |
Surface Area of a Right Hollow cylinder formula |
||
| \( A_s \;=\; h + 2 \cdot \pi \cdot (R^2 - r^2 ) \) | ||
| Symbol | English | Metric |
| \( A_s \) = surface area (bottom, top, side) | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( R \) = outside radius | \( in \) | \( mm \) |
| \( r \) = inside radius | \( in \) | \( mm \) |