Final Velocity Formula |
||
|
\( v_f \;=\; v_i + a \cdot t \) (Final Velocity) \( v_i \;=\; v_f + a \cdot t \) \( a \;=\; \dfrac{ v_f + v_i }{ t } \) \( t \;=\; \dfrac{ v_f - v_i }{ a } \) |
||
| Symbol | English | Metric |
| \(v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( a \) = acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( t \) = time | \(sec \) | \( s \) |
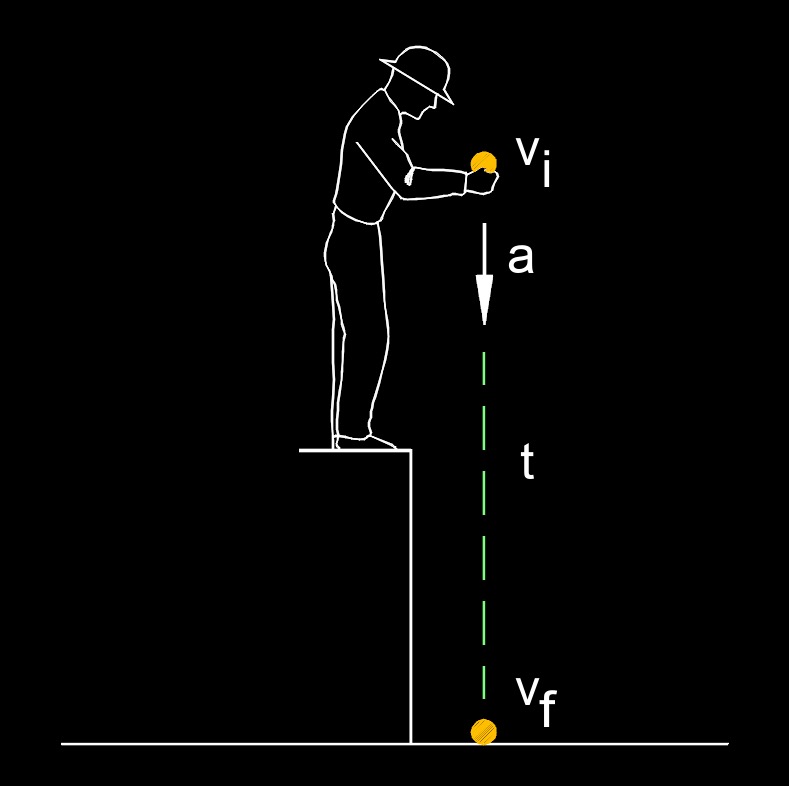Final velocity, abbreviated as \(v_f\), is the ending point of motion.
Final Velocity Formula |
||
|
\( v_f \;=\; 2 \cdot \bar {v} - v_i \) (Final Velocity) \( v \;=\; \dfrac{ v_f + v_i }{ 2 }\) \( v_i \;=\; 2 \cdot \bar {v} - v_f \) |
||
| Symbol | English | Metric |
| \( v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( \bar {v} \) = average velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |