Constant Angular Acceleration Formula |
||
|
\( \omega_f \;=\; \omega_i + \alpha \cdot t \) (Constant Angular Acceleration) \( \omega_i \;=\; \omega_f - \alpha \cdot t \) \( \alpha \;=\; \dfrac{ \omega_f - \omega_i }{ t }\) \( t \;=\; \dfrac{ \omega_f - \omega_i }{ \alpha }\) |
||
| Units | English | Metric |
| \( \omega_f \) (Greek symbol omega) = final angular velocity | \(deg / sec\) | \(rad / s\) |
| \( \omega_i \) (Greek symbol omega) = initial angular velocity | \(deg / sec\) | \(rad / s\) |
| \( \alpha \) (Greek symbol alpha) = angular acceleration | \(deg / sec^2\) | \(rad / s^2\) |
| \( t \) = time | \(sec\) | \(s\) |
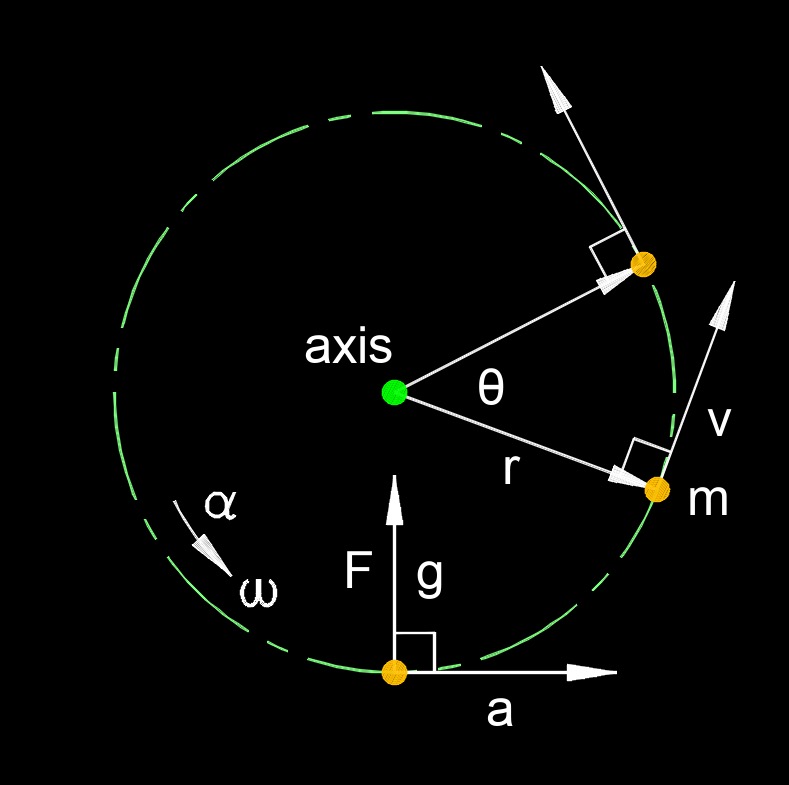Constant angular acceleration, abbreviated as \(\omega\) (Greek symbol omega), of an object is the constant rate at which the angular velocity changes with respect to time. It refers to a situation in rotational motion where an object or particle undergoes uniform and unchanging changes in its angular velocity over a specific period of time. Angular acceleration, measures how quickly the angular velocity of an object changes as it rotates. In other words, if an object is experiencing constant angular acceleration, it means that its rate of rotation is changing at a constant rate.
Key Points about Constant Angular Acceleration
Increasing Angular Velocity - If the angular acceleration is positive, it means the object is speeding up its rotation. This occurs when a torque or force is applied to the object in the direction of its rotation.
Decreasing Angular Velocity - If the angular acceleration is negative, it means the object is slowing down its rotation. This can occur when a torque or force is applied in the opposite direction of the object's rotation.
Constant angular acceleration is a fundamental concept in rotational dynamics and is often used to describe the behavior of objects like wheels, gears, and other rotating systems when subjected to external torques or forces. It is analogous to constant linear acceleration in translational motion, where an object's velocity changes at a constant rate.
