Skip to main content

Axial Stiffness

 

Axial Stiffness Formula

\( k \;=\;  \dfrac{ F }{ \delta }\)     (Axial Stiffness)

\( F \;=\;  k \cdot \delta  \)

\( \delta \;=\;  \dfrac{ F }{ k }\)
Symbol English Metric
\( k \) = Stiffness \(lbf\) \(N\)
\( F \) = Applied Force \(lbf\) \(N\)
\( \delta \)  (Greek symbol delta) = Deflection \(in\) \(mm\)

axial stiffness 1Axial stiffness, abbreviated as k, is the ability of a structure or component to resist deformation or displacement along its axial or longitudinal direction.  It is a measure of the resistance to axial loads or forces applied parallel to the longitudinal axis of the object.  In mechanical engineering and structural analysis, axial stiffness is typically quantified by the axial stiffness coefficient or axial stiffness constant.  This coefficient represents the relationship between the axial force applied to a structure and the resulting axial displacement or elongation.

Axial Stiffness for a Body in Tension Formula

  • Tension describes the pulling force exerted by each end of a string, cable, chain, or similar one-dimensional continuous object, or by each end of a rod, truss member, or similar three-dimensional object.

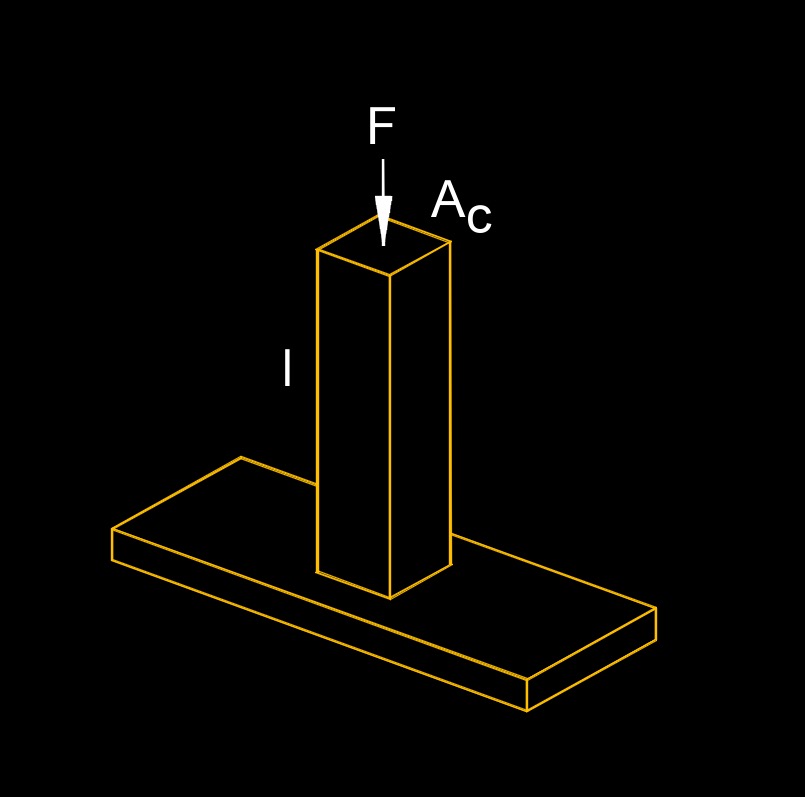
\( k \;=\;  \dfrac{ A_c \cdot E }{ l }\)     (Axial Stiffness)

\( A_c \;=\; \dfrac{  k \cdot l }{ E }\)

\( E \;=\; \dfrac{  k \cdot l }{ A_c }\)

\( l \;=\; \dfrac{  A_c \cdot E }{ k }\)
Symbol English Metric
\( k \) = Stiffness \(lbf\) \(N\)
\( A_c \) = Area Cross-section \(in^2\) \(mm^2\)
\( E \) = Young's Modulus \(lbf\;/\;in^2\) \(Pa\)
\( l \) = Length of Body \(in\) \(mm\)

The axial stiffness of a structure or component depends on its material properties, geometrical configuration, cross-sectional area, and boundary conditions.  It is typically determined through analytical calculations, numerical simulations, or experimental testing.  Engineers and designers consider axial stiffness to ensure structural integrity, optimize performance, and meet design requirements in various fields of engineering.

Axial Stiffness Various Applications
Structural Engineering  -  In the design of buildings, bridges, and other structures, axial stiffness is a crucial factor in determining the stability, load bearing capacity, and overall structural behavior.  It influences factors like deflection, buckling, and the ability to resist axial loads, such as the weight of the structure or external forces.
Mechanical Systems  -  Axial stiffness plays a role in mechanical systems that involve axial loads, such as shafts, columns, springs, and support structures.  The stiffness of these components affects their ability to transmit forces, resist deformation, and maintain alignment under axial loads.
Vibrational Analysis  -  In vibration analysis and dynamics, the axial stiffness of components or systems influences their natural frequencies, mode shapes, and response to dynamic loads.  It determines how much an object elongates or contracts in response to vibrational forces, impacting the overall dynamic behavior.
Manufacturing and Assembly  -  Axial stiffness is considered in manufacturing and assembly processes to ensure proper alignment, fit, and functioning of components that experience axial loads or forces.  It helps prevent undesired deflections, misalignments, or excessive deformations during operation.

Piping Designer Logo 1