Law of Conservation of Linear Momentum

Tags: Momentum Laws of Physics Law of Conservation

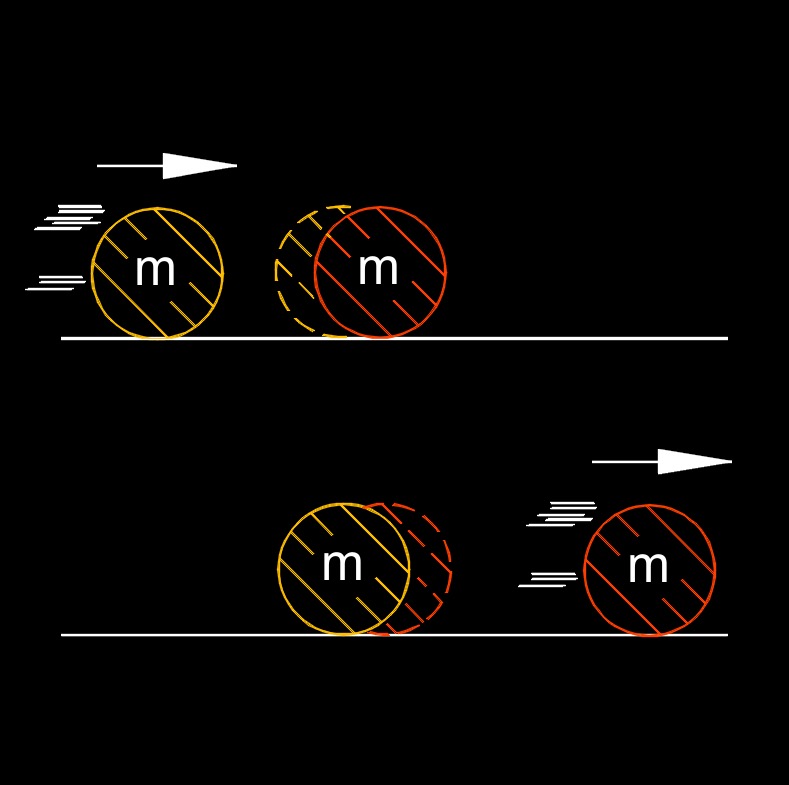Law of conservation of linear momentum states if the net external force acting on a system of bodies is zero, then the momentum of the system remains constant.  According to this law the absence of external forces, the total momentum before an event or interaction is equal to the total momentum after the event or interaction.  This means that the combined momentum of all objects within the system remains constant over time.

This law finds application in various areas of physics, such as collisions, explosions, and interactions between objects.  It is particularly useful in analyzing and predicting the motion and outcomes of such events.  It's important to note that this law applies to isolated systems, where no external forces are acting.  In real world scenarios, it may be challenging to find completely isolated systems due to the presence of external influences such as friction or air resistance.  However, the law is still valuable in providing insights and predictions in situations where external forces can be neglected or are negligible.

 

law of conservation of linear momentum formula
\(\large{ \overrightarrow{p} =  m \; \overrightarrow{v}  }\)     (Law of Conservation of Linear Momentum) \(\large{ m = \frac{ \overrightarrow{p} }{ \overrightarrow{v}  }  }\) \(\large{ \overrightarrow{v} = \frac{ \overrightarrow{p} }{ m }  }\)
Symbol	English	Metric
\(\large{ \overrightarrow{p} }\) = linear momentum	\(\large{\frac{lbm-ft}{sec}}\)	\(\large{\frac{kg-m}{s}}\)
\(\large{ m }\) = mass	\(\large{lbm}\)	\(\large{kg}\)
\(\large{ \overrightarrow{v} }\) = linear velocity	\(\large{\frac{ft}{sec}}\)	\(\large{\frac{m}{s}}\)