Skip to main content

Trajectory of a Projectile

Trajectory of a projectile is the curved path given an initial velocity and is acted on by gravity. The projectile is acted upon by both vertical and horizontal motion along the trajectory.

Trajectory of a Projectile formula
$y = d \; tan \; \theta - ( g \; d^2 \;/\; 2 \; v_0^2 \; cos^2 ( \theta ) \;)$
Symbol	English	Metric
$y$ = vertical position	$ft$	$deg$
$\theta$ = angle of the initial vertical from x-axis	$deg$	$rad$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$d$ = horizontal position	$ft$	$m$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$

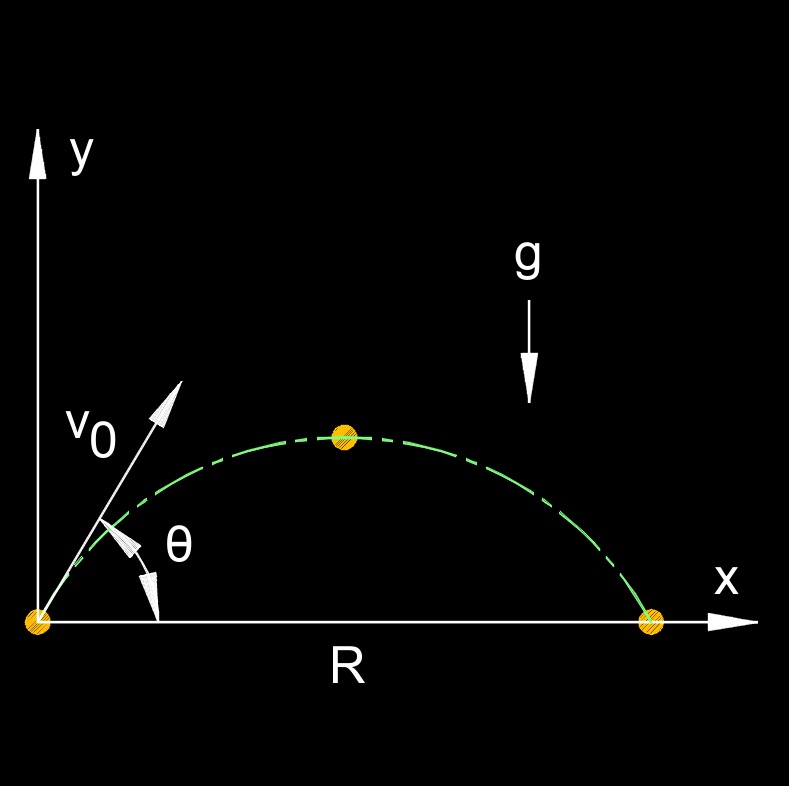
horizontal range of a Projectile formula
$R = v_0^2 \; sin \; 2 (\theta) \;/\; g$
Symbol	English	Metric
$R$ = horizontal range	$ft$	$\ m$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$\theta$ = vertical angle	$deg$	$rad$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$

Launch Velocity of a Projectile formula
$v_0 = \sqrt{ R \; g \;/\; sin\; 2 \;( \theta ) }$
Symbol	English	Metric
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$R$ = horizontal range	$ft$	$m$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$\theta$ = vertical angle	$deg$	$rad$

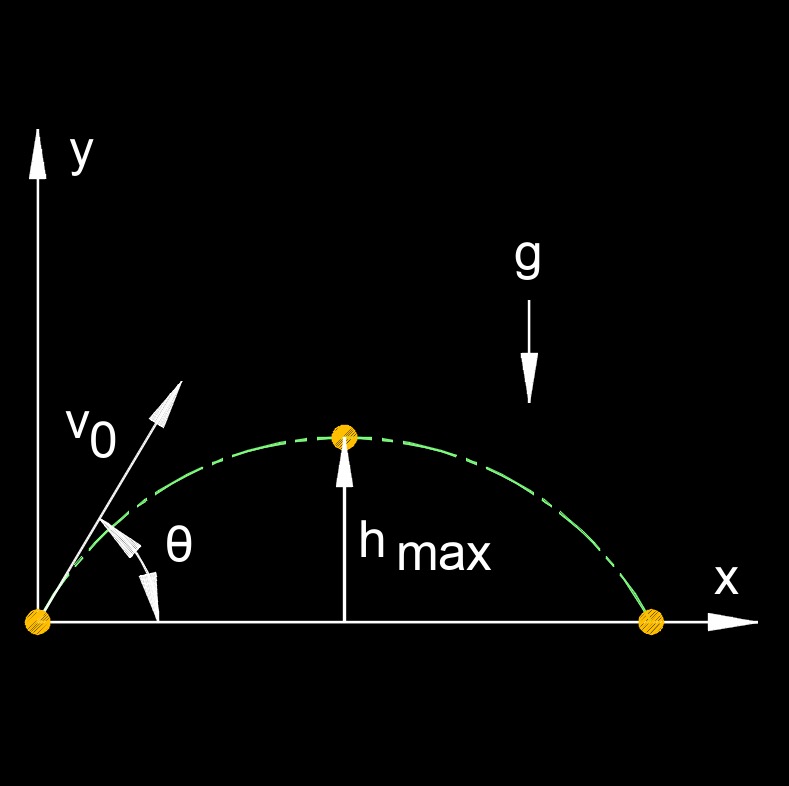
Maximum Height of a Projectile formula
$h_{max} = v_0 \; sin^2 \; (\theta) \;/\; 2 \; g$
Symbol	English	Metric
$h_{max}$ = maximum height	$ft$	$m$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$\theta$ = vertical angle	$deg$	$rad$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$

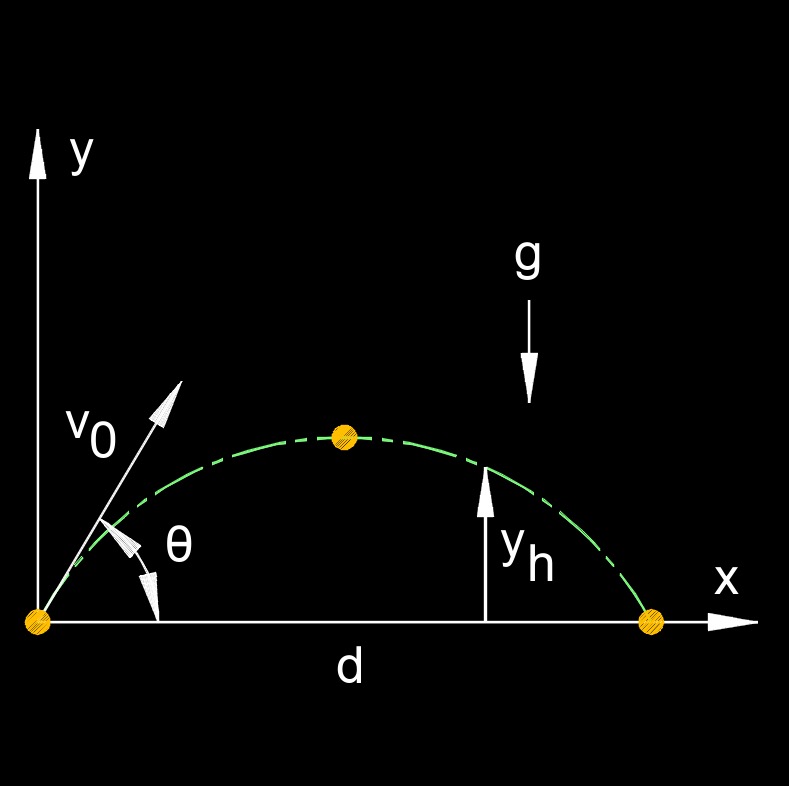
Projectile Clearing an Object formula
$y_h = ( d \; v_{0y} \;/\; v_{0x} ) - [\; \frac{1}{2} \; g \; ( x^2\;/\;v_{0x}^2 ) \;]$
Symbol	English	Metric
$y_h$ = vertical position	$ft$	$m$
$d$ = horizontal position	$ft$	$m$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$\theta$ = angle of the initial vertical from x-axis	$deg$	$rad$

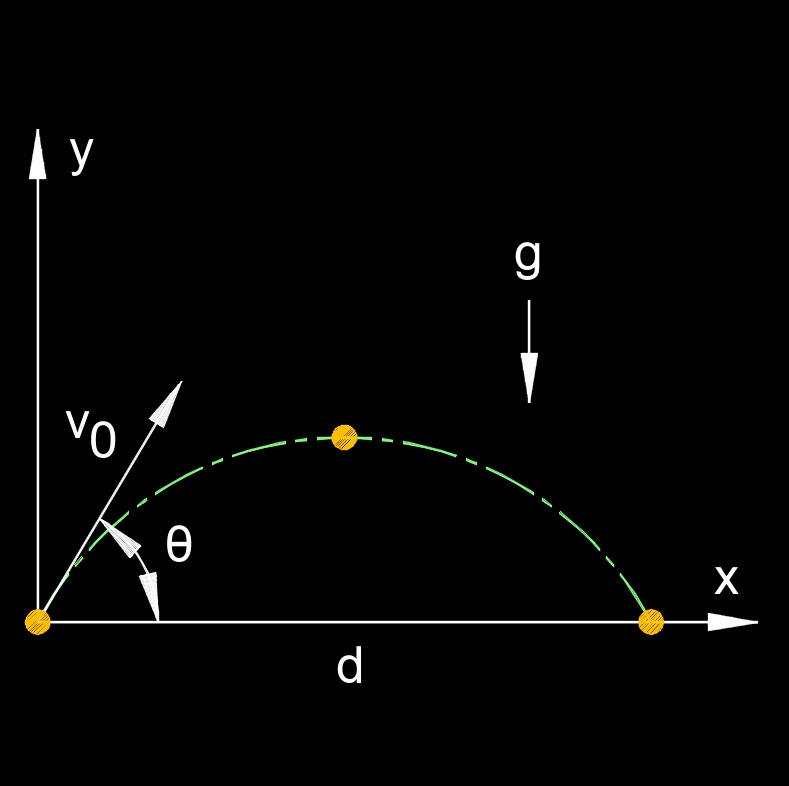
Projectile Launch Angle formula
$\theta = \frac{ 1 }{ 2 } \; sin^{-1} \left( g\; d \;/\; v_0^2 \right)$
Symbol	English	Metric
$\theta$ = angle of the initial vertical from x-axis	$deg$	$rad$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$d$ = horizontal position	$ft$	$m$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$

Time of Flight of a Projectile formula
$t = 2 \; v_0 \; sin (\theta) \;/\; g$
Symbol	English	Metric
$t$ = time	$sec$	$\ s$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$\theta$ = vertical angle	$deg$	$rad$

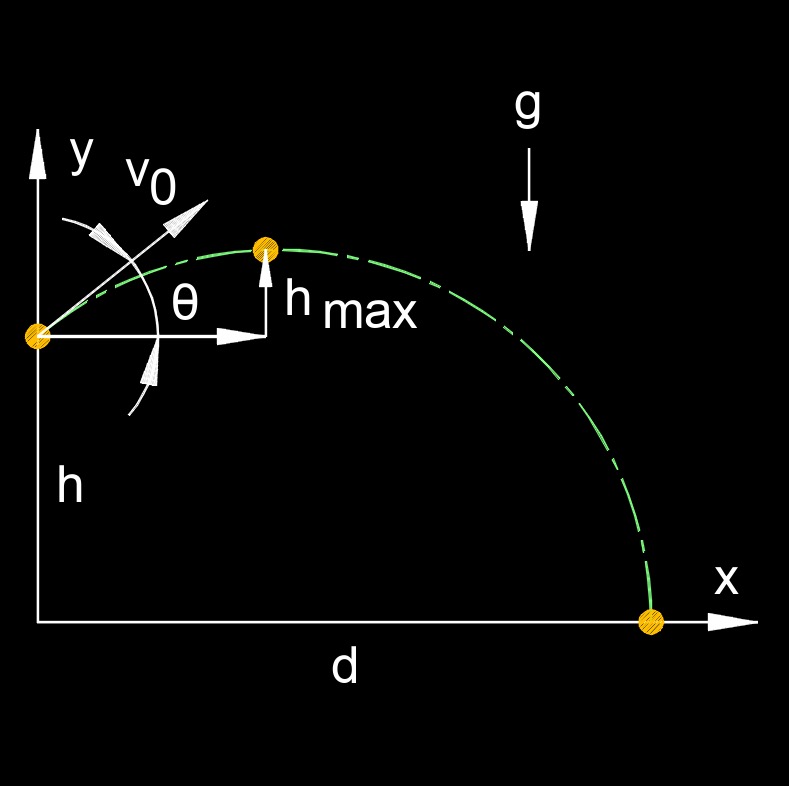
Trajectory of a Projectile on a Hill formulas
$t = ( 2 \; v_{0h} \;/\; g ) \pm \sqrt{ ( v_{0h}^2 \;/\; g^2 ) - ( 2 \;h \;/\; g ) }$ $d = v_{0d} \; t$ $h = v_{0h} \; t - \frac{1}{2} \; g \; t^2$
Symbol	English	Metric
$t$ = time	$sec$	$s$
$g$ = gravitational acceleration	$ft\;/\;sec^2$	$m\;/\;s^2$
$v_0$ = launch velocity	$ft\;/\;sec$	$m\;/\;s$
$\theta$ = vertical angle	$rad$	$rad$

Similar Articles

Latest Articles