Final Velocity Formula |
||
|
\( v_f \;=\; v_i + a \cdot t \) (Final Velocity) \( v_i \;=\; v_f + a \cdot t \) \( a \;=\; \dfrac{ v_f + v_i }{ t } \) \( t \;=\; \dfrac{ v_f - v_i }{ a } \) |
||
| Symbol | English | Metric |
| \(v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( a \) = acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( t \) = time | \(sec \) | \( s \) |
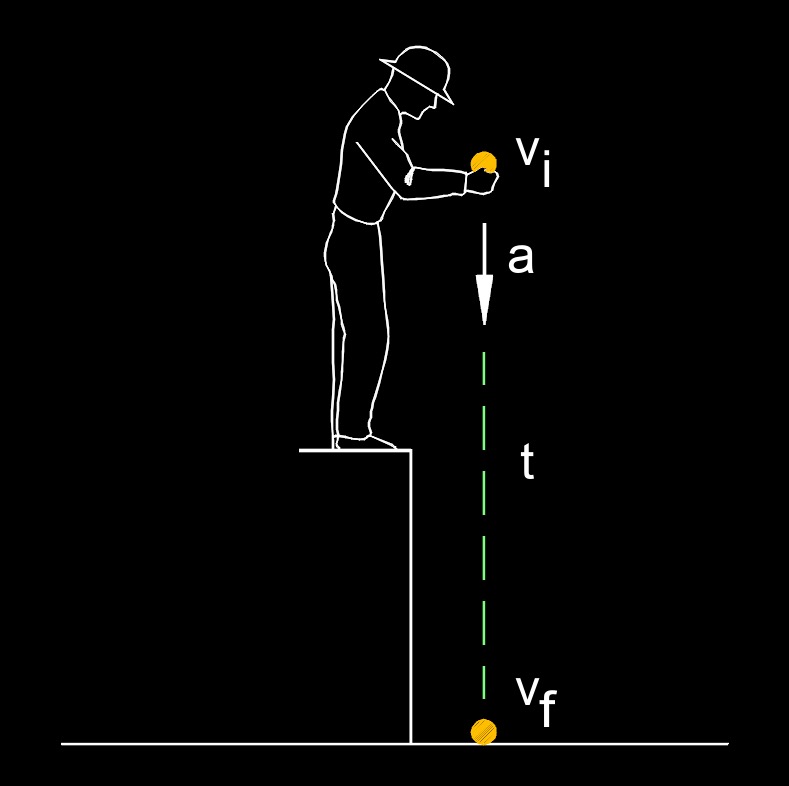Final velocity, abbreviated as \(v_f \), is the velocity an object has at the end of a motion or at a specific point in time after it has undergone acceleration or other changes in motion. It reflects both the speed and direction of the object at that moment. Final velocity depends on the initial velocity, the acceleration experienced by the object, and the time over which the acceleration acts. It is a variable in kinematic equations and is used to predict the outcome of motion, calculate stopping distances, or determine energy changes in a system. Essentially, it represents the object’s motion state at the conclusion of a given interval or event.
Final Velocity Formula |
||
|
\( v_f \;=\; 2 \cdot \bar {v} - v_i \) (Final Velocity) \( v \;=\; \dfrac{ v_f + v_i }{ 2 }\) \( v_i \;=\; 2 \cdot \bar {v} - v_f \) |
||
| Symbol | English | Metric |
| \( v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( \bar {v} \) = average velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |