Velocity Gradient
Velocity gradient formula |
||
|
\( \nu \;=\; \dfrac{ dv }{ dx }\) (Velocity Gradient) \( dv \;=\; \nu \cdot dx \) \( dx \;=\; \dfrac{ dv }{ \nu } \) |
||
| Symbol | English | Metric |
| \( \nu \) (Greek symbol nu) = Velocity Gradient | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( dv\) = Infinitesimally Small Change in Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( dx \) = Imperceptible Distance Perpendicular Between Two Layers of Fluid | \(in\) | \(mm\) |
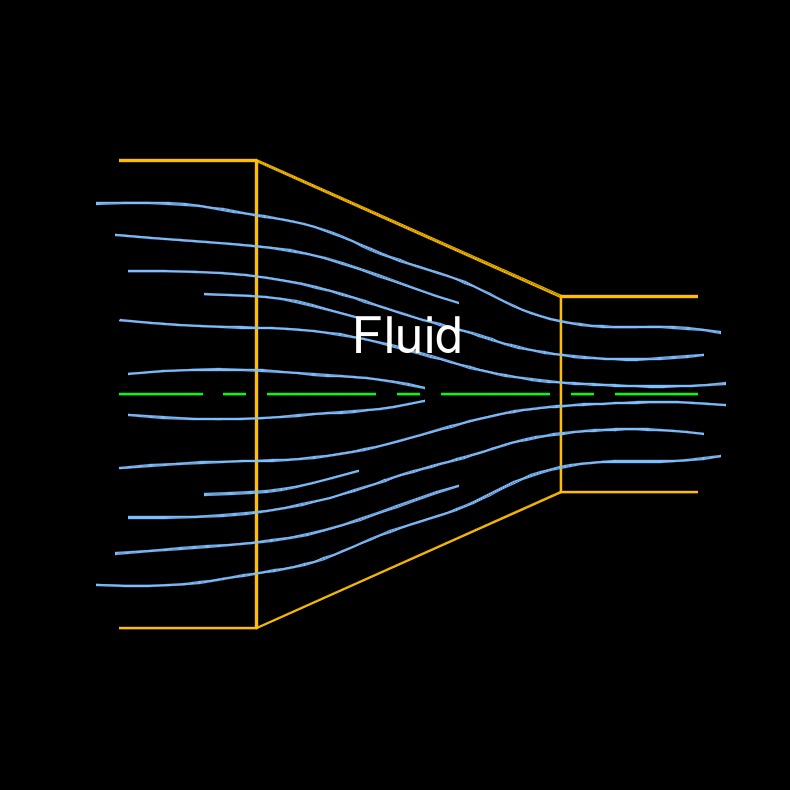
Velocity gradient, abbreviated as \(\nu\) (Greek symbol nu), is a measure of how the velocity of a fluid changes from one point to another within the flow field. It describes the rate at which velocity varies with position, usually perpendicular to the direction of flow. In fluid mechanics, the velocity gradient is important because it indicates how layers of fluid move relative to each other, which directly relates to shear stress and viscosity. A larger velocity gradient means the fluid layers are sliding past each other more quickly, leading to greater internal friction and higher shear forces. This concept is fundamental in understanding laminar flow, turbulence, and the overall behavior of real fluids.

