Kinetic friction coefficient formula |
||
|
\( \mu_k \;=\; \dfrac{ f_k }{ F_n }\) (Kinetic Friction Coefficient) \( f_k \;=\; \mu_k \cdot F_n \) \( F_n \;=\; \dfrac{ f_k }{ \mu_k }\) |
||
| Symbol | English | Metric |
| \( \mu_k \) (Greek symbol mu) = Kinetic Friction Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( f_k \) = Kinetic Friction | \( lbf \) | \(N\) |
| \( F_n \) = Normal Force | \( lbf \) | \(N\) |
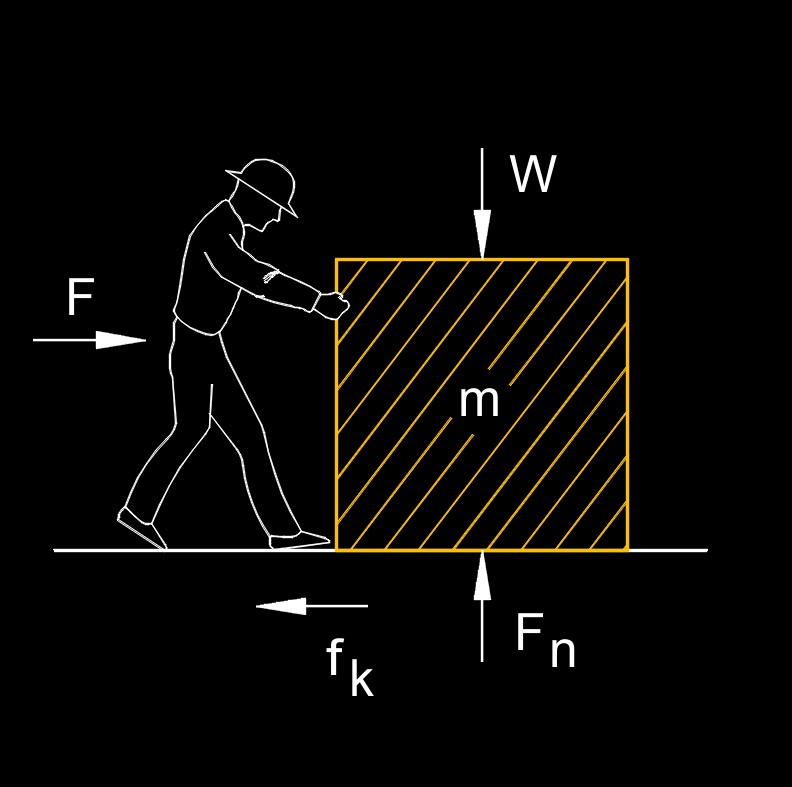Kinetic friction coefficient, abbreviated as \(\mu_k\), a dimensionless number, also called coefficient of kinetic friction or dynamic friction coefficient, is the amount of force that resists motion at a constant velocity. It describes the amount of frictional force that opposes the relative motion between two surfaces in contact, when they are already in motion. It quantifies the frictional resistance experienced by an object as it slides or moves across another surface.
The kinetic friction coefficient is used to calculate the frictional force in situations where objects are sliding on surfaces. Engineers and designers take it into consideration when analyzing and designing systems involving relative motion, such as braking systems, conveyor belts, and vehicle tires on roads.
Key Points about Kinetic Friction Coefficient
- It is generally smaller than the static friction coefficient between the same materials.
- It is relatively constant for a given pair of materials in motion, regardless of the sliding speed (within certain limits).
- The kinetic friction coefficient depends on the nature of the materials in contact, surface roughness, and other factors.
- It is an important parameter in engineering and physics, as it helps predict the frictional forces that must be overcome in various mechanical systems.
