Wavelength Velocity
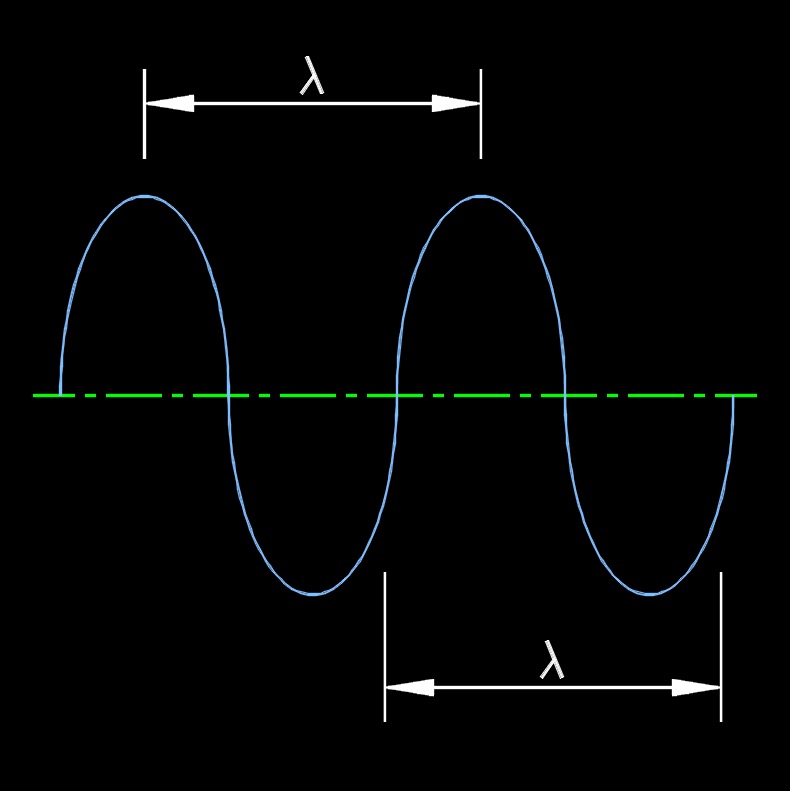Wavelength and velocity are both properties of waves, but they refer to different aspects:
Wavelength - This is the distance between two consecutive points that are in phase on a wave. In simple terms, it’s the length of one complete wave cycle, often measured from peak to peak or trough to trough.
Velocity - This refers to the speed at which the wave travels through a medium. It is the rate at which energy or information is transmitted by the wave.
This equation shows that if you know the frequency and wavelength of a wave, you can determine its velocity, and vice versa. For example, in sound waves, the velocity depends on the medium (air, water, etc.), while for electromagnetic waves like light, the velocity can vary depending on whether it's traveling through a vacuum or another medium like glass.
Wavelength Velocity formula |
||
|
\( v_w \;=\; f \;/\; \lambda \) (Wavelength Velocity) \( f \;=\; v_w \; \lambda \) \( \lambda \;=\; f \;/\; v_w \) |
||
| Symbol | English | Metric |
| \( v_w \) = Wavelength Velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( f \) = Frequency | \(Hz\) | \(Hz\) |
| \( \lambda \) (Greek symbol lambda) = Wavelength | \(ft\) | \(m\) |
