Hydraulic Head

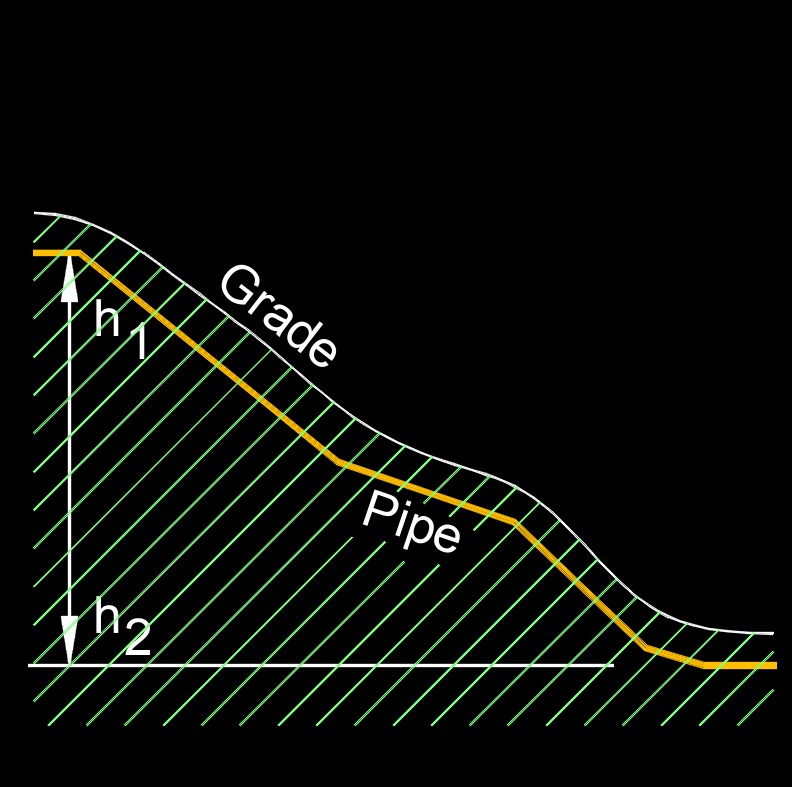Hydraulic head, abbreviated as h, is the measurement mechanical energy due to pressure of a fluid from a higher elevation to a lower elevation.  It is a fundamental concept in fluid mechanics and is commonly used in the fields of hydrology, hydrogeology, and hydraulic engineering. 

The hydraulic head is a useful concept for understanding and analyzing fluid flow behavior.  It determines the direction of fluid flow, with fluids generally flowing from regions of higher hydraulic head to regions of lower hydraulic head.  The difference in hydraulic head between two points is known as the hydraulic gradient, which drives the flow of fluids.

In hydrogeology, hydraulic head is commonly used to describe the level or position of groundwater within an aquifer.  It helps in characterizing groundwater flow patterns, estimating flow rates, and predicting the movement of contaminants or pollutants in the subsurface.  It's important to note that hydraulic head is based on the assumption of steady state flow conditions and may not fully capture the transient behavior of fluid systems or account for factors such as viscosity, flow resistance, or the presence of boundaries or obstacles that can affect flow dynamics.

 

Hydraulic head formula
\( h = p \;/\; g \; \rho \)     (Hydraulic Head) \( p = h \; g \; \rho \) \( g =  p \;/\; \rho \; h \) \( \rho = p \;/\; h \; g \)
Symbol	English	Metric
\( h \)= Head	\( ft \)	\( m \)
\( p \) = Pressure	\(lbf \;/\; in^2\)	\(N \;/\; m^2\)
\( g \) = Gravitational Acceleration	\(ft \;/\; sec^2\)	\(m \;/\; s^2\)
\( \rho \)  (Greek symbol rho) = Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)