Heat Transfer by Conduction Through a Plane Wall Formula |
||
| \( Q_c \;=\; \dfrac{ - k \cdot A_c \cdot ( T_2 - T_1 ) }{ L }\) | ||
| Symbol | English | Metric |
| \(Q_c \) = heat transfer by conduction | \(Btu\;/\;hr\) | \(W\) |
| \(A_c \) = area cross-section | \(in^2\) | \(mm^2\) |
| \( T_1 \) = temperature of one surface of the wall | \(^\circ F\) | \(^\circ K\) |
| \( T_2 \) = temperature of the other surface of the wall | \(^\circ F\) | \(^\circ K\) |
| \( k \) = thermal conductivity | \(Btu\;/\;hr-ft-F\) | \(W\;/\;m-K\) |
| \( L \) = material thickness | \(in\) | \(mm\) |
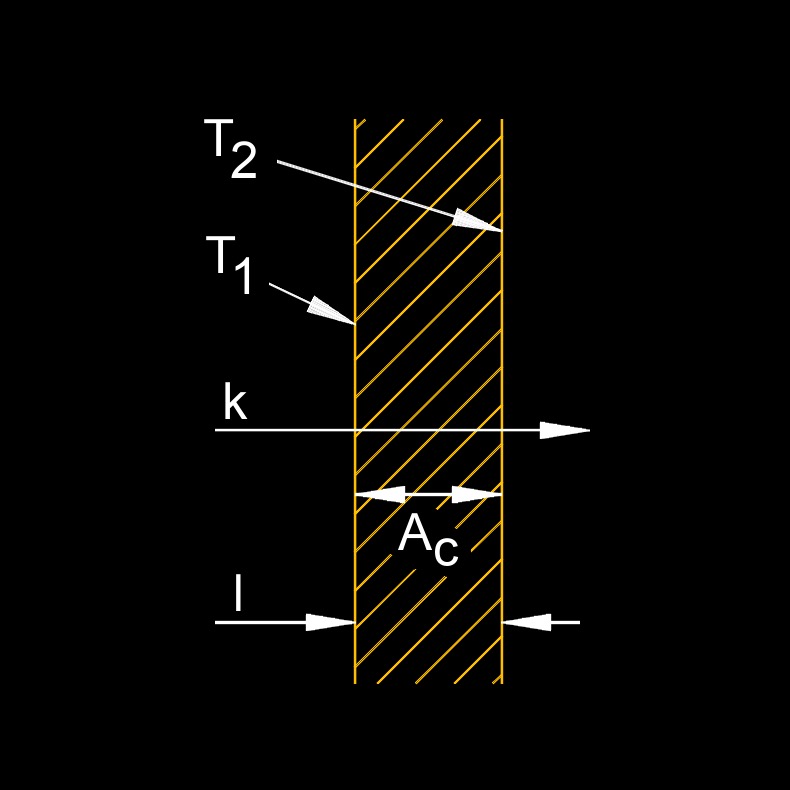
Heat transfer by conduction through a plane wall, abbreviated as \(Q_c \), is the process in which thermal energy moves through a flat, solid material due to a temperature difference between its two sides. When one surface of the wall is at a higher temperature and the opposite surface is at a lower temperature, heat naturally flows from the hot side to the cold side. This transfer happens at the molecular level: faster moving, energetic particles on the hot side collide with and transfer energy to slower moving particles toward the cold side. The wall’s thickness, thermal conductivity, surface area, and the temperature difference across it all affect how quickly heat flows. Conduction through a plane wall is commonly analyzed using Fourier’s law, which quantifies this heat flow and helps engineers calculate insulation needs, energy loss, and temperature distribution in buildings, machinery, and many types of equipment.
Heat Transfer by Conduction Through a Cylindrical Wall Formula |
||
| \( Q_c \;=\; \dfrac{ 2 \cdot \pi \cdot k \cdot l \cdot ( T_1 - T_2 ) }{ ln \cdot \left( \dfrac{ r_2 }{ r_1 } \right) }\) | ||
| Symbol | English | Metric |
| \( Q_c \) = heat transfer by conduction | \(Btu\;/\;hr\) | \(W\) |
| \( A_c \) = area cross-section | \(in^2\) | \(mm^2\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r_1 \) = radius of one surface of the wall | \(in\) | \(mm\) |
| \( r_2 \) = radius of the other surface of the wall | \(in\) | \(mm\) |
| \( T_1 \) = temperature of one surface of the wall | \(^\circ F\) | \(^\circ K\) |
| \( T_2 \) = temperature of the other surface of the wall | \(^\circ F\) | \(^\circ K\) |
| \( k \) = thermal conductivity | \(Btu\;/\;hr-ft-F\) | \(W\;/\;m-K\) |
| \( l \) = material thickness | \(in\) | \(mm\) |
