Angular Momentum in Terms of Magnitude Formula |
||
| \( L \;=\; m \cdot v \cdot r \cdot sin(\theta) \) | ||
| Symbol | English | Metric |
| \( L \) = Magnitude of the Angular Momentum | \(lbm - ft^2 \;/\; sec\) | \(kg - m^2 \;/\; s\) |
| \( m \) = Mass of Particles | \(lbm\) | \(kg\) |
| \( v \) = Magnitude of the Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( r \) = Distance from the Axis of Rotation | \(ft\) | \(m\) |
| \( \theta \) = Angle Between the Position Vector\(r\) and the Velocity Vector \(v\) | \(deg\) | \(rad\) |
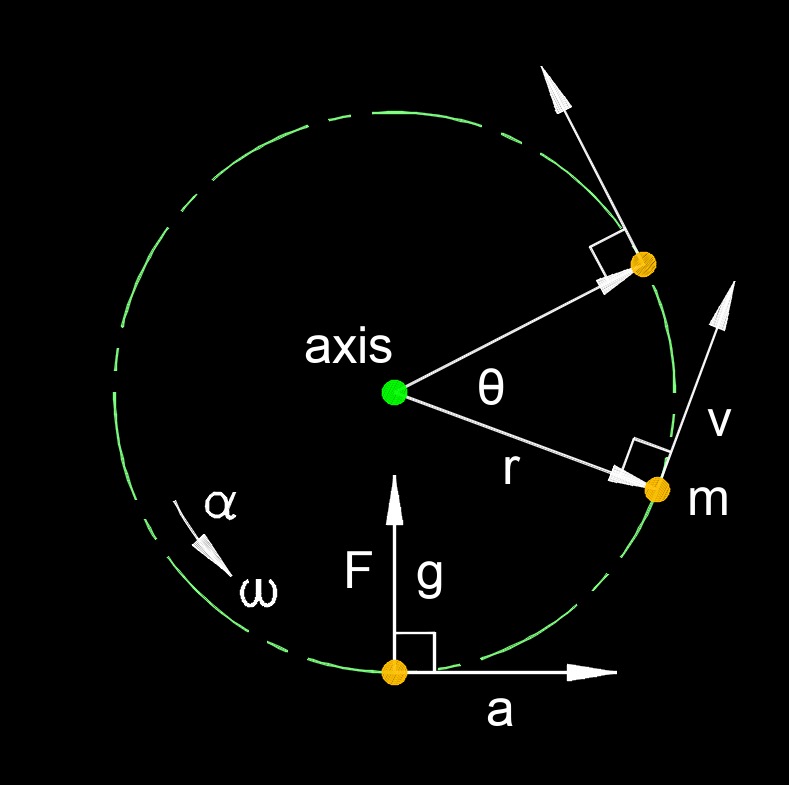
Angular momentum in terms of its magnitude, is a scalar quantity that measures the amount of rotational motion possessed by a system and is defined as the product of the system's moment of inertia and its angular velocity. In all cases, the magnitude quantifies how much leverage the momentum has about the chosen point or axis, increasing with greater mass, faster speed, larger distance from the axis, or a distribution of mass farther from the rotation axis, and it remains conserved in magnitude for isolated systems with no external torques acting. The greater the mass, velocity, or distance from the axis, the larger the angular momentum, indicating a stronger tendency for the object to continue rotating.
