Wetting Perimeter of a Trapezoidal Channel Formula |
||
| \( P_w \;=\; b + 2 \cdot \left(\; \left( \dfrac{ t - b }{ 2 } \right)^2 + h^2\; \right)^\frac{1}{2} \) | ||
| Symbol | English | Metric |
| \( P_w \) = Wetting Perimeter | \( ft \) | \( m \) |
| \( b \) = Bottom Width of Liquid | \( ft \) | \( m \) |
| \( t \) = Top Width of Liquid | \( ft \) | \( m \) |
| \( h \) = Fluid Depth | \( ft \) | \( m \) |
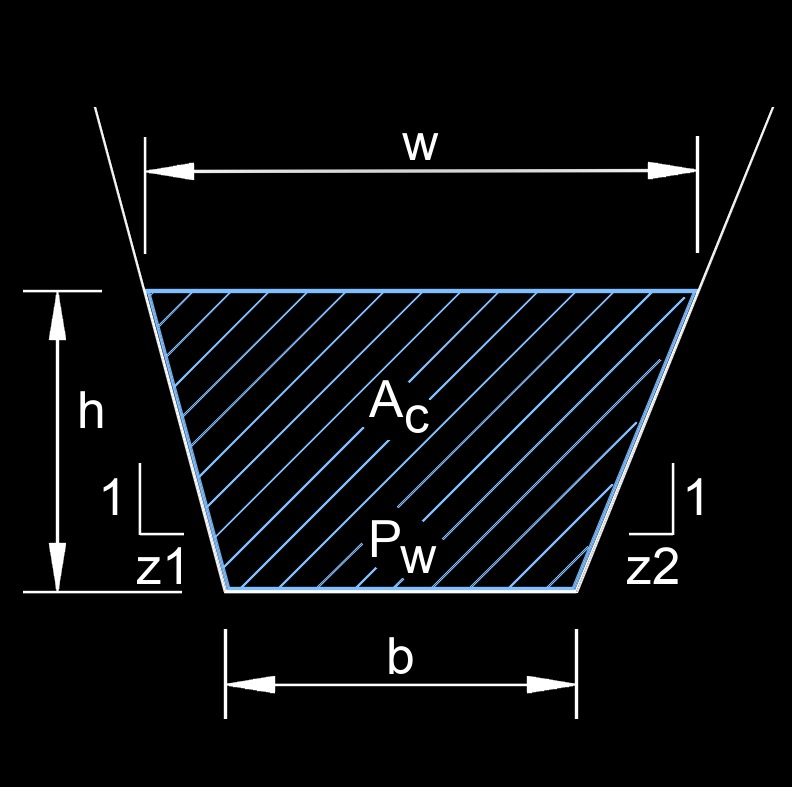For a trapezoidal open channel, the wetted perimeter is the sum of the bottom width of the channel and the lengths of the two sloped side walls that are in contact with the flowing water. Since trapezoidal channels have sloping sides, the wetted perimeter calculation is slightly more complex than for a rectangular channel. The length of each sloped side in contact with the water can be found using the Pythagorean theorem, as it forms the hypotenuse of a right-angled triangle with a vertical side and a horizontal side. This wetted perimeter is essential for hydraulic calculations, particularly in determining the hydraulic radius, which is used in formulas like Manning's equation to predict flow characteristics such as velocity and discharge in open channels.
