Wetting Perimeter of a Triangle Channel Formula |
||
| \( P_w \;=\; (2 \cdot h) \cdot ( 1 + z^2 )^\frac{1}{2} \) | ||
| Symbol | English | Metric |
| \( P_w \) = Wetting Perimeter | \( ft \) | \( m \) |
| \( h \) = Fluid Depth | \( ft \) | \( m \) |
| \( z \) = Horizontal Side Slope | \( ft \) | \( m \) |
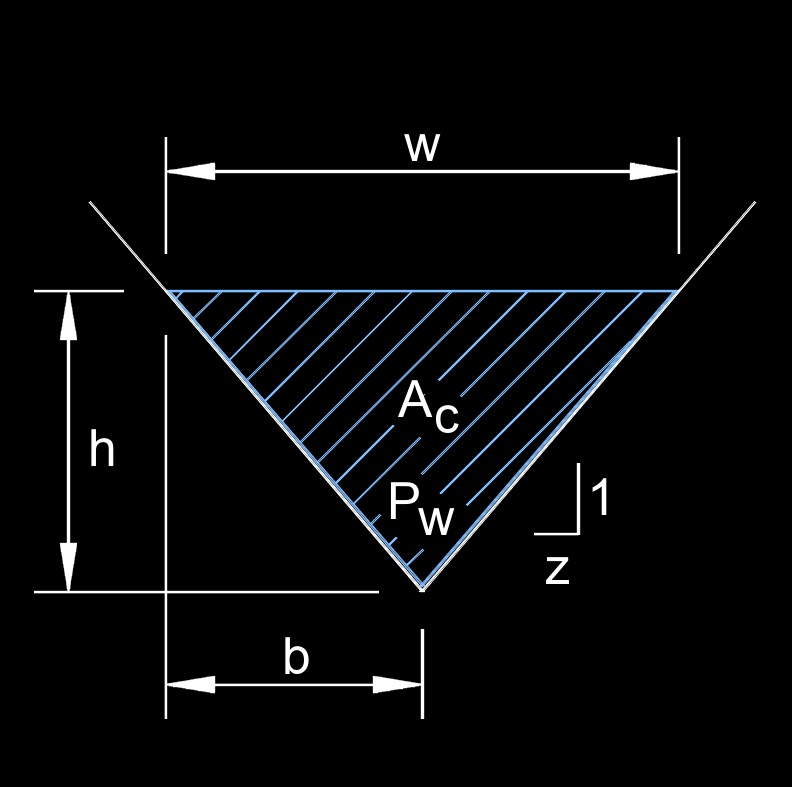For a triangular open channel, the wetted perimeter is the sum of the lengths of the two sloping sides that are in contact with the flowing fluid. Unlike rectangular or trapezoidal channels, a triangular channel does not have a flat bottom in contact with the water; instead, the bottom is a single point where the two sloping sides meet. Each sloping side forms the hypotenuse of a right angled triangle, with a vertical side and a horizontal side. This value is used for hydraulic calculations, particularly in determining the hydraulic radius, which is the ratio of the flow's cross-sectional area to the wetted perimeter. The hydraulic radius is then used in formulas like Manning's equation to predict flow velocity and discharge within the channel.
