Skip to main content

Unequal I Beam

Area of a Unequal I Beam Formula
A \;=\;  b\cdot s  +  h\cdot t  +  w\cdot s 
Symbol English Metric
A = area in^2 mm^2
h = height in mm
s = thickness in mm
t = thickness in mm
b = width in mm
w = width in mm

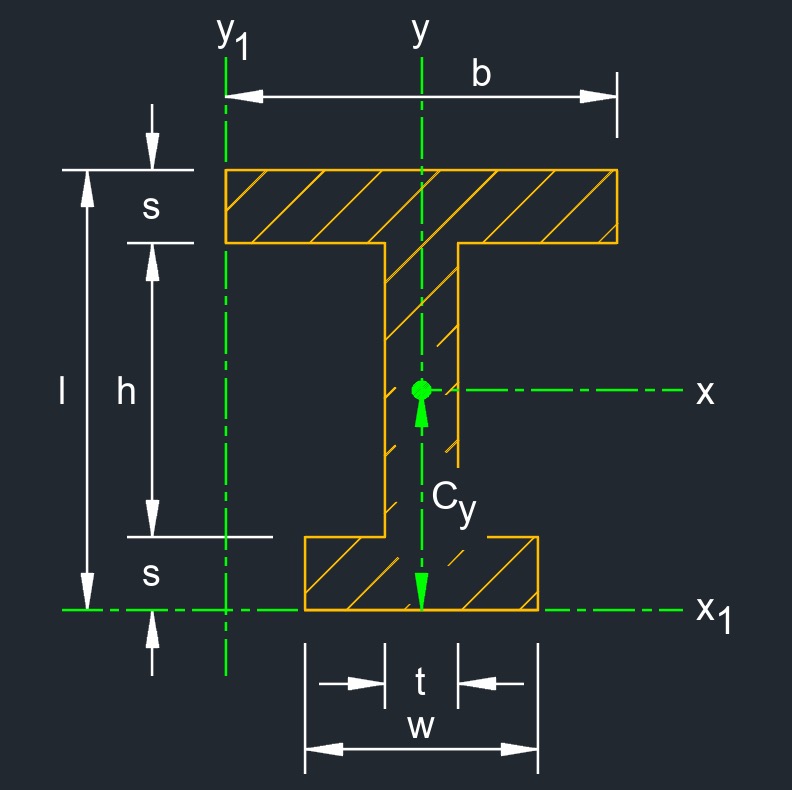I beam unequal 1An unequal I-beam, also called unequal I-section or unequal beam, is a type of structural steel member with an I-shaped cross-sectional profile where the flanges (horizontal top and bottom parts) have different widths.  This results in an asymmetrical shape where one flange is wider than the other.  The unequal I-beam is designed to accommodate specific load and structural requirements where the loads are not symmetrically distributed.  Unequal I-beams are commonly used in situations where the loads, spans, and other design considerations vary along the length of the beam.  The wider flange typically corresponds to the side that experiences higher loads or needs to provide greater resistance to bending and shear forces.

Distance from Centroid of a Unequal I Beam formulas

C_x =  0 

C_y \;=\;    l -  \dfrac{ 1 }{2\;A} \cdot \left[  t\cdot l^2  +  s^2 \cdot \left( b - t \right)  +  s\cdot \left(w - t \right) \cdot \left(2\cdot l -  s \right)  \right]   
Symbol English Metric
C = distance from centroid in mm
A = area in^2 mm^2
l = height in mm
s = thickness in mm
t = thickness in mm
b = width in mm
w = width in mm

I beam unequal 1The design of an unequal I-beam involves calculating the dimensions of both flanges and the web (the vertical part connecting the flanges) to ensure that the beam can effectively handle the applied loads while maintaining structural stability.  Engineering considerations such as bending moments, shear forces, and deflection are taken into account during the design process. 

Piping Designer Logo 1

 

 

 

 

Elastic Section Modulus of a Unequal I Beam formulas

S_{x} \;=\;  \dfrac{ I_x }{ C_y}  

S_{y} \;=\;  \dfrac{ I_y }{ C_x}  
Symbol English Metric
S = elastic section modulus in^3 mm^3
C = distance from centroid in mm
I = moment of inertia in^4 mm^4

 I beam unequal 1

 

 

 

 

 

 

 

Perimeter of a Unequal I Beam formula
P \;=\;  2 \cdot \left( w  +  b  +  l - t  \right)  
Symbol English Metric
P = perimeter in mm
l = height in mm
t = thickness in mm
b = width in mm
w = width in mm

 I beam unequal 1

 

 

 

 

 

 

 

Radius of Gyration of a Unequal I Beam formulas

k_{x} \;=\;    \dfrac{    \dfrac{1}{3}  \cdot   \left[  b \cdot  \left(l - C_y \right)^3  +  w \cdot C_{y}{^3}  - \left(b - t \right)   \cdot   \left(l - C_y  - s \right)^3   -  \left(w  -  t \right)   \cdot  \left(C_y  +  s \right)^3    \right]         }{     b\cdot s  + h\cdot t  + w\cdot s}     

k_{y} \;=\;     \dfrac{  \sqrt{  s \cdot \left(s^2  +  3 \right) \cdot  \left(w -  t \right)^3  +  2\cdot h\cdot t^3 }            }{          2\cdot \sqrt{6}  \cdot  \sqrt{w\cdot s  +  b\cdot s  +  h\cdot t }  }     
Symbol English Metric
k = radius of gyration in mm
C = distance from centroid in mm
h = height in mm
l = height in mm
s = thickness in mm
t = thickness in mm
b = width in mm
w = width in mm

 I beam unequal 1

 

 

 

 

 

 

 

 

 

 

 

 

 

Second Moment of Area of a Unequal I Beam formulas

I_x \;=\;  \dfrac{1}{3}   \cdot  \left[    b \cdot  \left(l - C_y \right)^3  +  w \cdot C_{y}{^3}  - \left(b - t \right) \left(l - C_y  - s \right)^3   -  \left(w  -  t \right)   \left(C_y -  s \right)^3    \right]    

I_y \;=\;   2 \cdot \left[ 2 \cdot \left(   \dfrac{1}{96} \cdot s^3 \cdot  \left(w - t \right)^3  +  \dfrac{1}{32} \cdot s \cdot \left(w -  t \right)^3   \right) +  \dfrac{h\cdot t^3}{24}      \right]   

I_z \;=\;   l_x  +  I_y  
Symbol English Metric
I = moment of inertia in^4 mm^4
C = distance from centroid in mm
h = height in mm
l = height in mm
s = thickness in mm
t = thickness in mm
b = width in mm
w = width in mm

I beam unequal 1 

 

 

 

 

 

 

 

 

 

 

 

 

 

Torsional Constant of a Unequal I Beam formula
J  \;=\;   \dfrac{ w\cdot s^3 +  b\cdot s^3  + \left( l - 5 \right) \cdot t^3  }{  3  }   
Symbol English Metric
J = torsional constant in^4 mm^4
l = height in mm
s = thickness in mm
t = thickness in mm
b = width in mm
w = width in mm

I beam unequal 1