Gauss's Law for Magnetism Formula |
||
| \( \triangledown \cdot B \;=\; 0 \) | ||
| Symbol | English | Metric |
| \( \triangledown \) = Represents Divergence (How Much a Field Spreads Out) | \(dimensionless\) |
\(dimensionless\)
|
| \( B \) = Magnetic Flux Density | \(G\) | \(T\) |
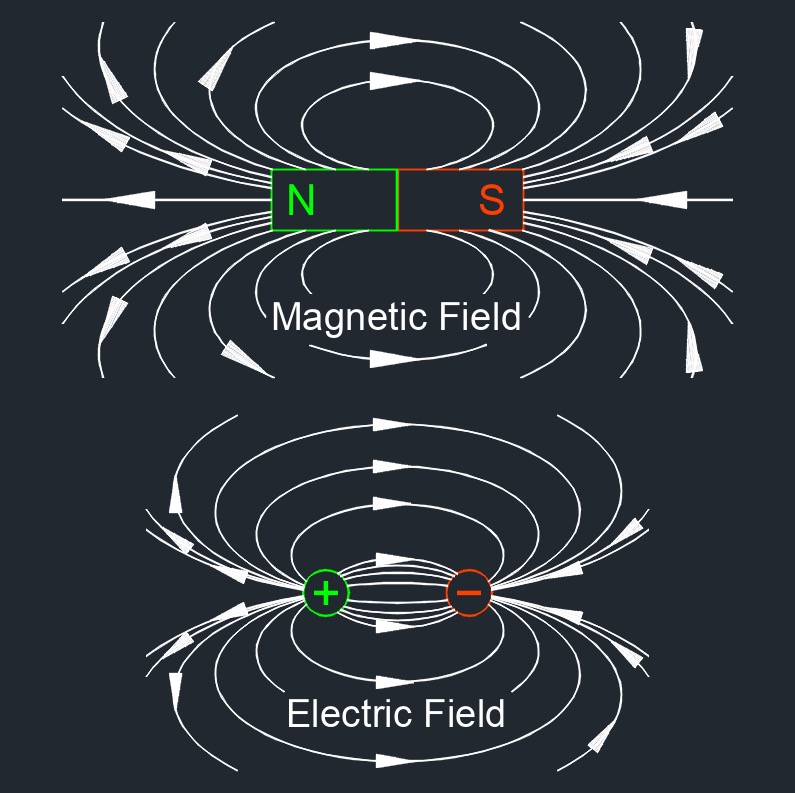Gauss’s law for magnetism states that the net electric flux through any closed surface is always zero. This law expresses the fundamental principle that magnetic monopoles do not exist in nature, meaning that magnetic field lines never begin or end at a single point charge as electric field lines do, instead, they always form continuous closed loops. In practical terms, this implies that every magnetic north pole is always accompanied by a south pole, and no isolated magnetic charges can be found. Gauss’s law for magnetism is essential for understanding how magnetic fields behave in space and emphasizes the inherent symmetry of magnetic field lines.
See Articles
