|
|
|
\( B_d \;=\; 1.075 \cdot \dfrac{ V^2 }{ a } \) (Braking Distance)
\( V \;=\; \sqrt{ \dfrac{ B_d \cdot a }{ 1.075} } \)
\( a \;=\; \dfrac{ V^2 \cdot 1.075 }{ B_d }\)
|
| Symbol |
English |
Metric |
| \( B_d \) = Braking Distance |
\(ft\) |
\(m\) |
| \( V \) = Design Speed |
\( ft \;/\; sec \) |
\(m \;/\; s\) |
| \( a \) = Deceleration Rate |
\( ft \;/\; sec \) |
\(m \;/\; s\) |
Breaking distance, abbreviated as \(B_d\), is the distance a vehicle travels from the moment the brakes are fully applied until the vehicle comes to a complete stop. It is a critical factor in understanding the overall stopping distance of a vehicle and is influenced by various factors, including vehicle speed, road conditions, vehicle weight, braking system efficiency, and tire grip. Braking distance consists of two main components: the initial portion where the vehicle is decelerating, and the latter portion where the vehicle is at a lower speed and is gradually coming to a stop.
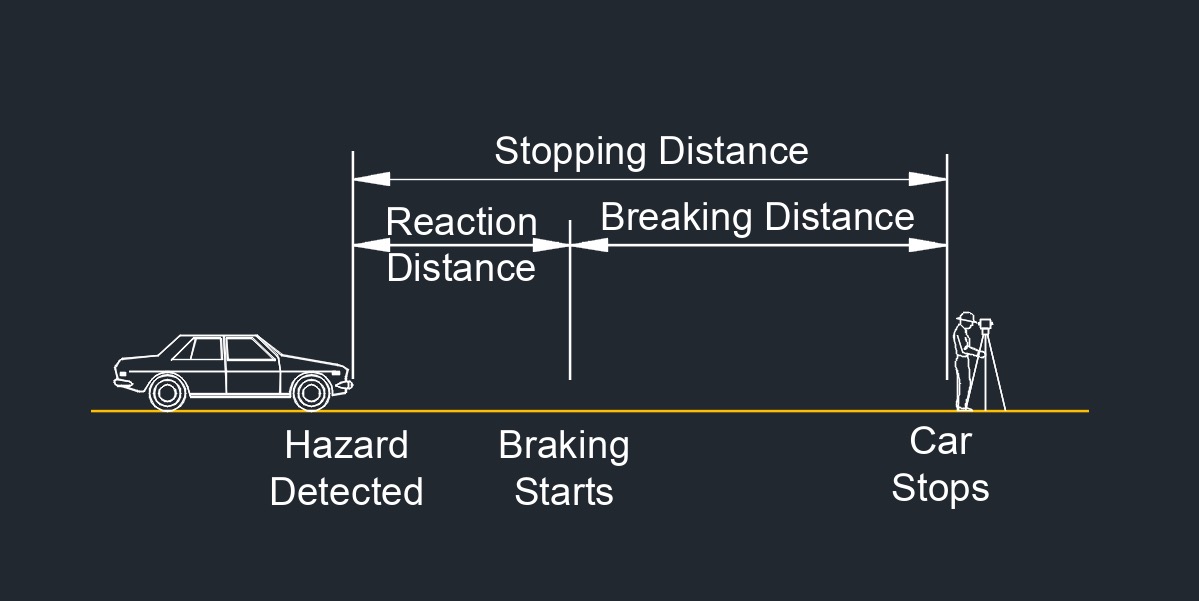
AASHTO Exhibit 3-1 Stopping Sight Distance
- Brake reaction distance predicated on a time of 2.5 s; deceleration.
- Rate of 11.2 \(ft/s^2\) used to determine calculated sight distance.
|
Design Speed
|
Design Speed Distance
|
Braking Distance on Level |
Stopping Sight Distance |
| Calculated |
Design |
| 15 |
55.1 |
21.6 |
76.7 |
80 |
| 20 |
73..5 |
38.4 |
111.9 |
115 |
| 25 |
91.9 |
60.0 |
151.9 |
155 |
| 30 |
110.3 |
86.4 |
196.7 |
200 |
| 35 |
128.6 |
117.6 |
246.2 |
250 |
| 40 |
147.0 |
153.6 |
300.6 |
305 |
| 45 |
165.4 |
194.4 |
359.8 |
360 |
| 50 |
183.8 |
240.0 |
423.8 |
425 |
| 55 |
202.1 |
290.3 |
492.4 |
495 |
| 60 |
220.5 |
345.5 |
566.0 |
570 |
| 65 |
238.9 |
4.505 |
644.4 |
645 |
| 70 |
257.3 |
470.3 |
727.6 |
730 |
| 75 |
275.6 |
539.9 |
815.5 |
820 |
| 80 |
294.0 |
614.3 |
908.3 |
910 |
Factors that Influence Braking Distance
Speed - Braking distance increases significantly with higher initial speeds. A vehicle traveling at a higher speed will require more distance to come to a complete stop.
Deceleration - The braking capability of a vehicle depends on its braking system, tire grip, and road conditions. A higher deceleration (stronger braking) reduces braking distance.
Road Conditions - Wet, icy, or slippery road surfaces reduce tire grip and increase braking distance.
Tire Condition - Worn or improperly inflated tires can affect braking efficiency and increase braking distance.
Vehicle Weight - Heavier vehicles have more
kinetic energy at a given speed, which requires more energy to stop, leading to a longer braking distance.
Brake System - The condition and effectiveness of a vehicle's brake system impact the braking performance and subsequently the braking distance.
It's important to note that braking distance is only one component of the overall stopping distance. The total stopping distance includes both the braking distance and the brake reaction distance, which is the distance traveled while the driver reacts to a hazard and initiates braking. Taking into account both components is crucial for ensuring safe driving and collision avoidance. Drivers should maintain a safe following distance from the vehicle in front of them to allow for sufficient Braking Distance, especially in adverse weather conditions or when driving at higher speeds.



