- See Article - Geometric Properties of Structural Shapes
area of a Square I Beam formula |
||
| \( A \;=\; w\cdot l - h \cdot \left( w - t \right) \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
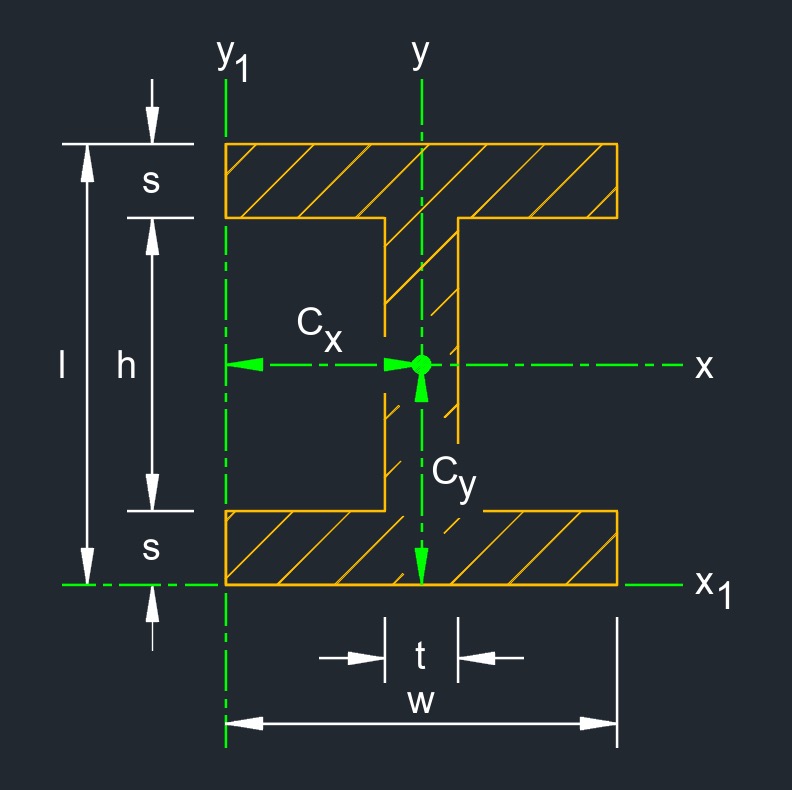Square I Beam, also called square hollow section (SHS) or square H-beam, is a type of structural steel member commonly used in construction and engineering applications. It belongs to the family of I-beams, which are named for their cross-sectional shape resembling the letter "I". However, in the case of a square I beam, the cross-sectional shape is a square rather than the traditional "I" shape.
Distance from Centroid of a Square I Beam formulas |
||
|
\( C_x \;=\; \dfrac{ w }{ 2 } \) \( C_y \;=\; \dfrac{ l }{ 2} \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
A square I beam consists of four equal-length sides that form a square shape. It has the same basic characteristics as a regular I-beam, such as its ability to support heavy loads and distribute weight efficiently. The square shape provides additional benefits, such as uniform load distribution and ease of connection with other structural components, making it suitable for various applications in building frames, bridges, industrial structures, and more.
Elastic Section Modulus of a Square I Beam formulas |
||
|
\( S_{x} \;=\; \dfrac{ I_{x} }{ C_{y} } \) \( S_{y} \;= \; \dfrac{ I_{y} }{ C_{x} } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Perimeter of a Square I Beam formula |
||
| \( P \;=\; 2 \cdot \left( 2\cdot w + l - t \right) \) | ||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Polar Moment of Inertia of a Square I Beam formulas |
||
|
\( J_{z} \;=\; I_{x} + I_{y}{^2} \) \( J_{z1} \;=\; I_{x1} + I_{y1}{^2} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Radius of Gyration of a Square I Beam formulas |
||
|
\( k_{x} \;=\; \sqrt{ \dfrac{ w\cdot l^3 - h^3 \cdot \left( w - t \right) }{ 12 \cdot \left [ w\cdot l - h \cdot \left( w - t \right) \right ] } } \) \( k_{y} \;=\; \sqrt{ \dfrac{ 2\cdot s\cdot w^3 + h\cdot t^3 }{ 12 \cdot \left [ w\cdot l - h \cdot \left( w - t \right) \right ] } } \) \( k_{z} \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \sqrt{ \dfrac { I_{x1} }{ A } } \) \( k_{y1} \;=\; \sqrt{ \dfrac { I_{y1} }{ A } } \) \( k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Second Moment of Area of a Square I Beam formulas |
||
|
\( I_{x} \;=\; \dfrac{ w\cdot l^3 - h^3 \cdot \left( w - t \right) }{12} \) \( I_{y} \;=\; \dfrac{ 2\cdot s\cdot w^3 + h\cdot t^3 }{12} \) \( I_{x1} \;=\; l_{x} + A\cdot C_y \) \( I_{y1} \;=\; l_{y} + A\cdot C_x \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Torsional Constant of a Square I Beam formula |
||
| \( J \;=\; \dfrac{ 2\cdot w\cdot t^3 + \left( l - s \right) \cdot t^3 }{ 3 } \) | ||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |