Hooke's Law formula |
||
|
\( F_s \;=\; - k_s \cdot ( x - x_0 ) \) (Hooke's Law) \( k_s \;=\; \dfrac{-F_s }{ x - x_0} \) \( x \;=\; x_0 - \dfrac{F_s }{ k_s} \) \( x_0 \;=\; \dfrac{F_s }{ k_s} + x \) |
||
| Symbol | English | Metric |
| \( F_s \) = Spring Force | \( lb_f \) | \( N \) |
| \( k_s \) = Spring Constant | \( lb_f \) | \( N \) |
| \( x \) = Distance from Equilibrium | \( in \) | \( mm \) |
| \( x_0 \) = Spring Equilibrium Position | \( in \) | \( mm \) |
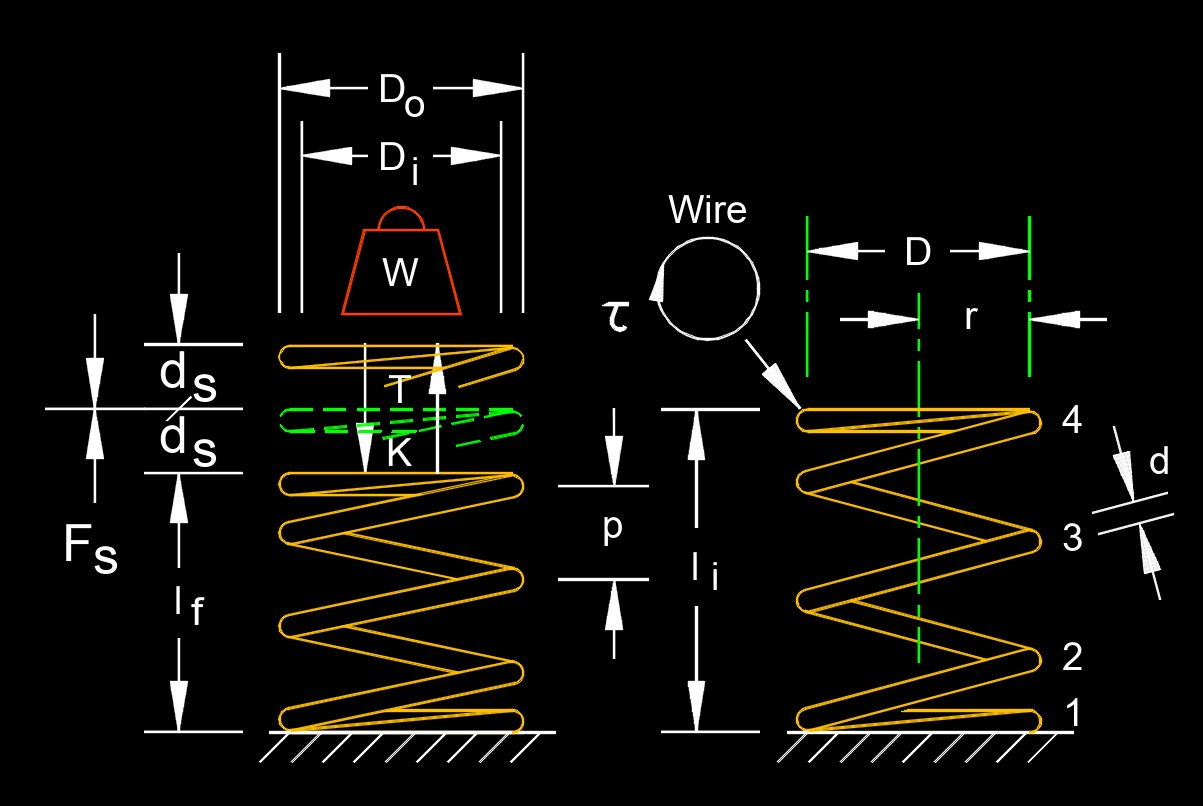Hooke's Law is a law of elasticity, abbreviated as F, also called spring force, describes the relationship between the force applied to a spring and the resulting displacement or deformation of the spring. It states that the force required to stretch or compress a spring is directly proportional to the displacement or change in length of the spring, as long as the elastic limit of the spring is not exceeded. In simpler terms, Hooke's law states that the force exerted by a spring is directly proportional to how far it is stretched or compressed. The negative sign in the equation indicates that the force exerted by the spring is opposite in direction to the displacement, meaning it acts to restore the spring back to its equilibrium position.
Hooke's law is widely applicable in physics and engineering. It is commonly used to model the behavior of springs, such as those found in mechanical systems, suspension systems, and various instruments. It forms the basis for understanding elasticity and provides a fundamental principle for studying the deformation of materials.
