Ellipse
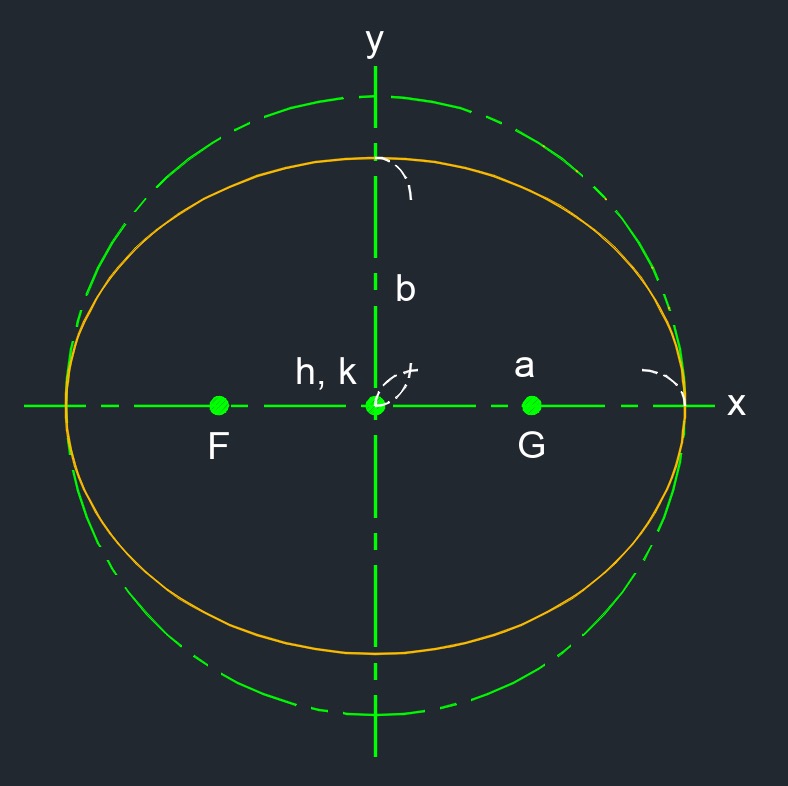
 Ellipse (a two-dimensional figure) is a conic section or a stretched circle. It is a flat plane curve that when adding togeather any two distances from any point on the ellipse to each of the foci will always equal the same.
Ellipse (a two-dimensional figure) is a conic section or a stretched circle. It is a flat plane curve that when adding togeather any two distances from any point on the ellipse to each of the foci will always equal the same.- Foci is a point used to define the conic section. F and G seperately are called "focus", both togeather are called "foci".
- The perimeter of an ellipse formula is an approximation that is about 5% of the true value as long as "a" is no more than 3 times longer than "b".
- Latus rectum is a line drawn perpencicular to the transverse axis of the ellipse and is passing through the foci of the ellipse.
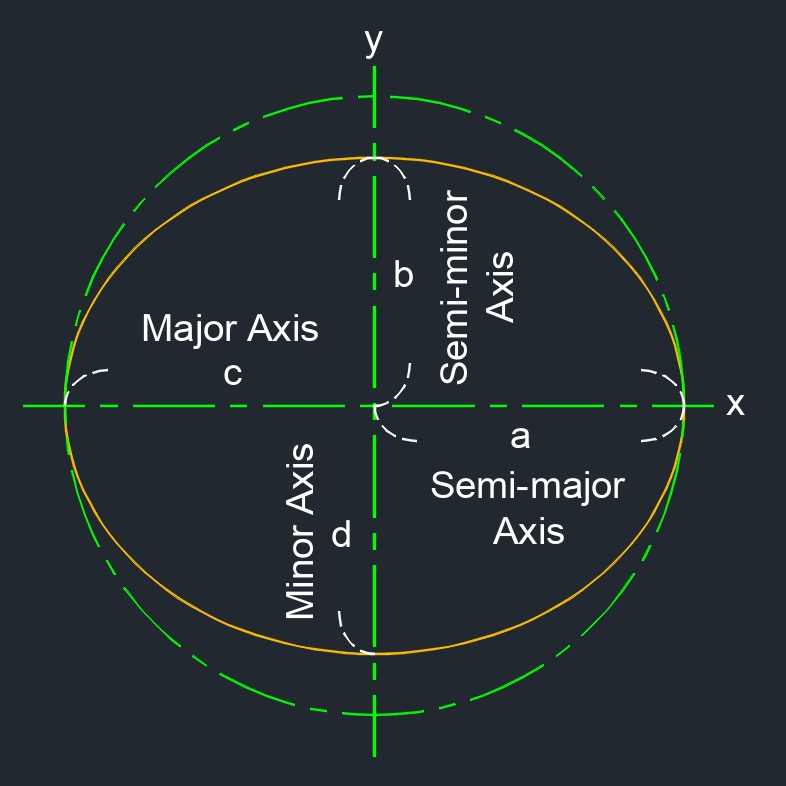
- The major axis is always the longest axis in an ellipse.
- The minor axis is always the shortest axis in an ellipse.
Standard Ellipse formulas |
||
|
\( \dfrac{ x^2}{a^2} + \dfrac{ y^2}{x^2} \;=\; 1 \) \( \left(\dfrac{ x}{a } \right)^2 + \left( \dfrac{ y}{x} \right)^2 \;=\; 1 \) \( \dfrac{ \left( x - h \right )^2 }{ a^2 } + \dfrac{ \left( y - k \right )^2 }{ b^2 } \;=\; 1 \) (Major Axis Horizontal) \( \dfrac{ \left( x - h \right )^2 }{ b^2 } + \dfrac{ \left( y - k \right )^2 }{ a^2 } \;=\; 1 \) (Major axis Vertical) |
||
| Symbol | English | Metric |
| \( x \) = horizontal coordinate of a point on the ellipse | \( in \) | \( mm \) |
| \( y \) = vertical coordinate of a point on the ellipse | \( in \) | \( mm \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( h \) and \(\large{ k }\) = center point of ellipse | \( in \) | \( mm \) |
Area of an Ellipse formula |
||
| \( A \;=\; \pi \cdot a \cdot b \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
Circumference of an Ellipse formula |
||
| \( C \;=\; 2 \cdot \pi \cdot \sqrt{ \dfrac{ a^2 + b^2 }{ 2 } } \) | ||
| Symbol | English | Metric |
| \( C \) = circumference | \( in \) | \( mm \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
eccentricity of an Ellipse formula |
||
|
\( \epsilon \;=\; \sqrt{ \dfrac{ a^2 - b^2 }{ a^2 } } \) \( \epsilon \;=\; \left( \dfrac{ 1 - b^2 }{ a^2 } \right)^{0.5} \) \( \epsilon \;=\; \sqrt{ 1 - \dfrac{ b^2 }{ a^2 } } \) |
||
| Symbol | English | Metric |
| \( \epsilon \) (Greek symbol epsilon) = eccentricity | \( dimensionless \) | \(3.141 592 653 ...\) |
| \( a \) = one half of the ellipse's major axis | \( in \) | \( mm \) |
| \( a \) = one half of the ellipse's minor axis | \( in \) | \( mm \) |
Perimeter of an Ellipse formulas
|
||
|
\( p \;\approx\; 2\cdot \pi \cdot \sqrt{ \dfrac{ 1}{2} \cdot \left(a^2 + b^2 \right) } \) \( p \;\approx\; 2 \cdot \pi \cdot \sqrt{ \dfrac{ a^2 + b^2}{2} }\) |
||
| Symbol | English | Metric |
| \( p \) = perimeter approximation | \( in \) | \( mm \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
Latus Rectum of an Ellipse formula |
||
| \( L \;=\; \dfrac{ 2 \cdot b^2 }{ a }\) | ||
| Symbol | English | Metric |
| \( L \) = Latus rectum | \( in \) | \( mm \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
Semi-major Axis Length of an Ellipse formula |
||
| \( a \;=\; \dfrac{ A }{ pi \cdot b }\) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
Semi-minor Axis Length of an Ellipse formula |
||
| \( b \;=\; \dfrac{ A }{ pi \cdot a }\) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |

