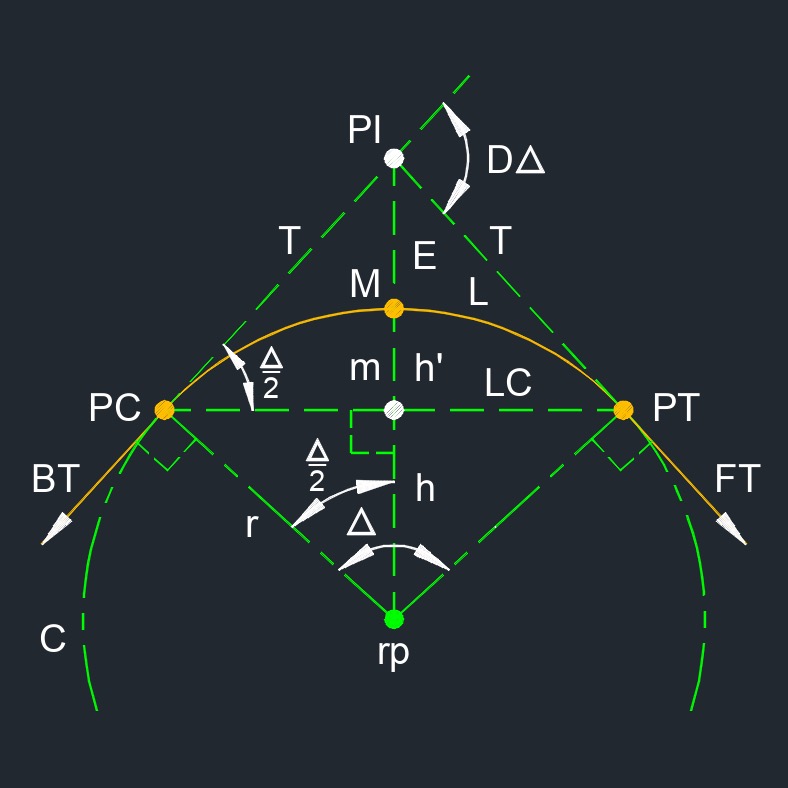
Chord of a Circle

Arc Length of a chord Formulas The arc length (l), is the total length of any circular curve measured along the arc, beginning at the curve PC (point on curve) to the end of the arc PT (point on tangent).
\( L \;=\; \Delta \cdot r \) \( L \;=\; \dfrac{ r \cdot \Delta \cdot \pi }{ 180 }\) \( L \;=\; \dfrac{ \Delta }{ 180 } \cdot 2 \cdot \pi \cdot r \)
Symbol	English	Metric
\( L \) = length	\( in \)	\( mm \)
\( \Delta \) = angle	\( deg \)	\( rad \)
\( \pi \) = Pi	\( 3.141 592 653 ...\)	\( 3.141 592 653 ...\)
\( r \) = radius	\( in \)	\( mm \)

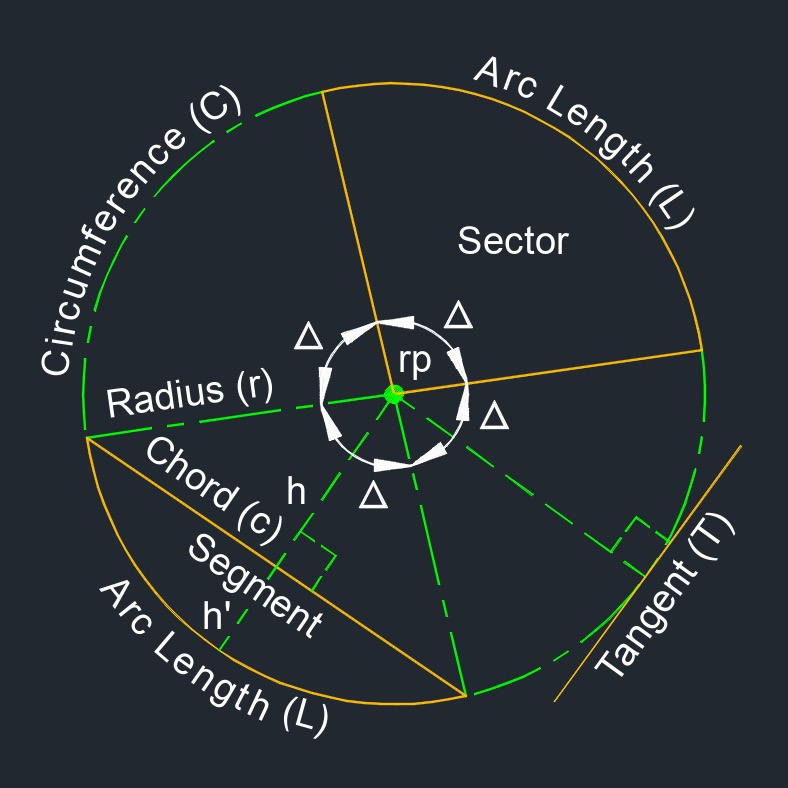
Chord (c), also called long chord (LC), is between any two points on a circular curve.
Angle (\(\Delta\)) - Two rays sharing a common point.
Back Tangent (BT) - The tangent line before the beginning of the curve.
Center (rp) - Having all points on the line circumference are at equal distance from the center point.
Circle - All points are at a fixed equal distance from a radius point (rp).
Circumference (C) - The outside of a circle or a complete circular arc.

Length of a chord Formulas The chord length (c), also called long chord (LC), is a straight line from the beginning of the curve PC (point on curve) to the end of the arc PT (point on tangent).
\( c \;=\; 2 \cdot r \cdot \sin \left( \dfrac{ \Delta}{2 } \right) \) \( c \;=\; 2 \cdot \sqrt{ r^2 - h^2 } \)
Symbol	English	Metric
\(\large{ c }\) = chord	\( in \)	\( mm \)
\(\large{ h }\) = chord circle center to midpoint distance	\( in \)	\( mm \)
\( \Delta \) = angle	\( deg \)	\( rad \)
\( r \) = radius	\( in \)	\( mm \)

Deflection Angle (D\(\Delta\)) - Deflection angle from full circular curve measured from tangent at PC or PT. The angles between a tangent and the ends of the chords from the PC.
External Distance (E) - Radial distance from PI to midpoint on a simple circular curve.
Forward Tangent (FT) - The tangent line after the ending of the curve.
Height (h) - Length of radius from radius center to midpoint of chord.
Height (h') - Length of radius from midpoint of chord to point on circular curve.
Length (L) - Total length of any circular curve measured along the arc.
Mid-point (M) - Center or halfway point of a line segment.

center of circle to chord midpoint Formula Length of radius (h) from radius center (rp) to midpoint of chord (c).
\( h \;=\; \sqrt{ r^2 - \dfrac{ L^2 }{ 4 } } \)
Symbol	English	Metric
\(\large{ h }\) = chord circle center to midpoint distance	\( in \)	\( mm \)
\(\large{ r }\) = circle radius	\( in \)	\( mm \)
\( L \) = length	\( in \)	\( mm \)
\(\large{ h' }\) = segment height	\( in \)	\( mm \)

Middle Ordinate (m) - The distance from the midpoint of the curve to the mid-point of the long chord.
Point of Curvature (PC) - The point at which a straight line begins to curve, the point tangency to the curve
Point of Intersection (PI) - The intersection of two tangent points or where two non-parallel lines intersect.
Point of Tangent (PT) - The point at which a curved line ends and the point tangency to the curve begins.
Radius (r) - Half the diameter of a circle.
Radius Point (rp) - Radius center point of circular curve.
Tangent (T) - A line that touches a curve at just one point such that it is perpendicular to a radius line of the curve.

chord midpoint to arc midpoint Formula Length of radius from midpoint of chord to point on circular curve in the segment.
\( h' \;=\; r - h \) \( h' \;=\; r \cdot \left( 1 - cos \left( \dfrac{ \Delta }{ 2} \right) \;\right) \)
Symbol	English	Metric
\(\large{ h' }\) = segment height	\( in \)	\( mm \)
\( \Delta \) = angle	\( deg \)	\( rad \)
\(\large{ h }\) = chord circle center to midpoint distance	\( in \)	\( mm \)
\(\large{ r }\) = circle radius	\( in \)	\( mm \)

External Distance to Arc Formula Radial distance (E) from point of intersection (PI) to midpoint on a circular curve.
\( E \;=\; T \cdot tan \left( \dfrac{\Delta }{ 4 } \right) \)
Symbol	English	Metric
\(\large{ E }\) = external distance	\( in \)	\( mm \)
\( \Delta \) = angle	\( deg \)	\( rad \)
\(\large{ T }\) = tangent length	\( in \)	\( mm \)