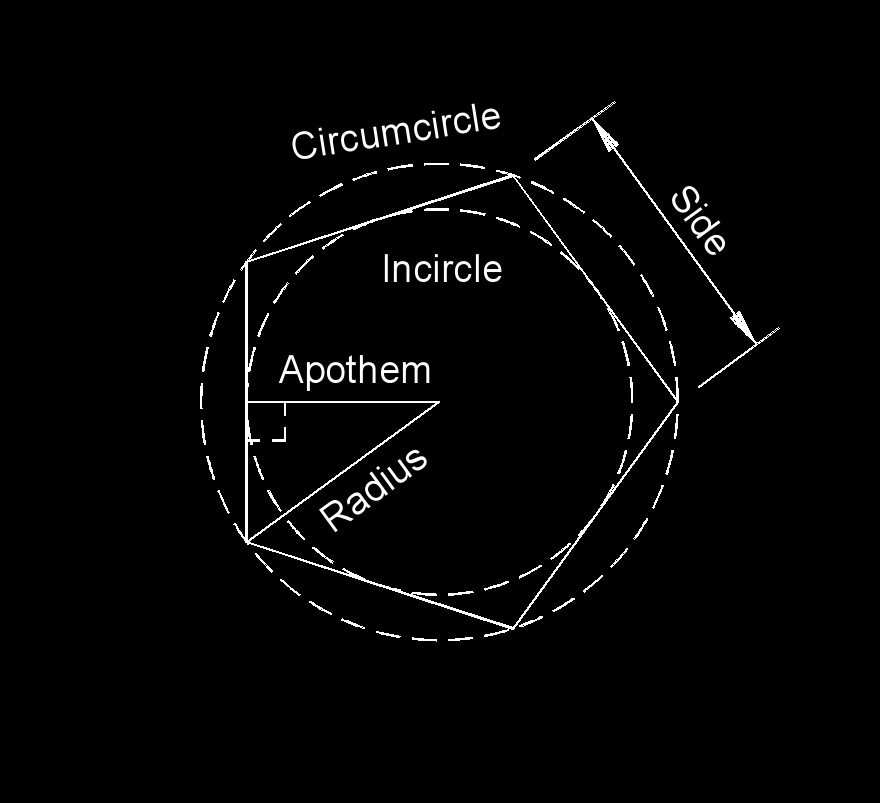Apothem is the length of a line perpendicular from the center to the midpoint of the side of a regular polygon.- A irregular polygon has no center so there can be no apothem.
Apothem Edge formula
|
| \(\large{A=\frac {s} {2 \;tan\; \left( \frac{180}{n} \right) } }\) |
| Symbol |
English |
Metric |
| \(\large{A}\) = apothem |
\(\large{in}\) |
\(\large{mm}\) |
| \(\large{s}\) = edge (side length) |
\(\large{in}\) |
\(\large{mm}\) |
| \(\large{n}\) = number of sides |
\(\large{dimensionless}\) |
| \(\large{tan}\) = tangent |
\(\large{deg}\) |
\(\large{rad}\) |
Apothem Radius formula
|
| \(\large{A= r \;cos\; {\left( \frac{180}{n} \right) } }\) |
| Symbol |
English |
Metric |
| \(\large{A}\) = apothem |
\(\large{in}\) |
\(\large{mm}\) |
| \(\large{cos}\) = cosine |
\(\large{deg}\) |
\(\large{rad}\) |
| \(\large{n}\) = number of sides |
\(\large{dimensionless}\) |
| \(\large{r}\) = radius |
\(\large{in}\) |
\(\large{mm}\) |
