Square Angle

See Article - Geometric Properties of Structural Shapes

area of a Square Channel formula
$A \;=\; t \cdot \left( 2\cdot w - t \right)$
Symbol	English	Metric
$A$ = area	$\large{ in^2 }$	$\large{ mm^2 }$
$t$ = thickness	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

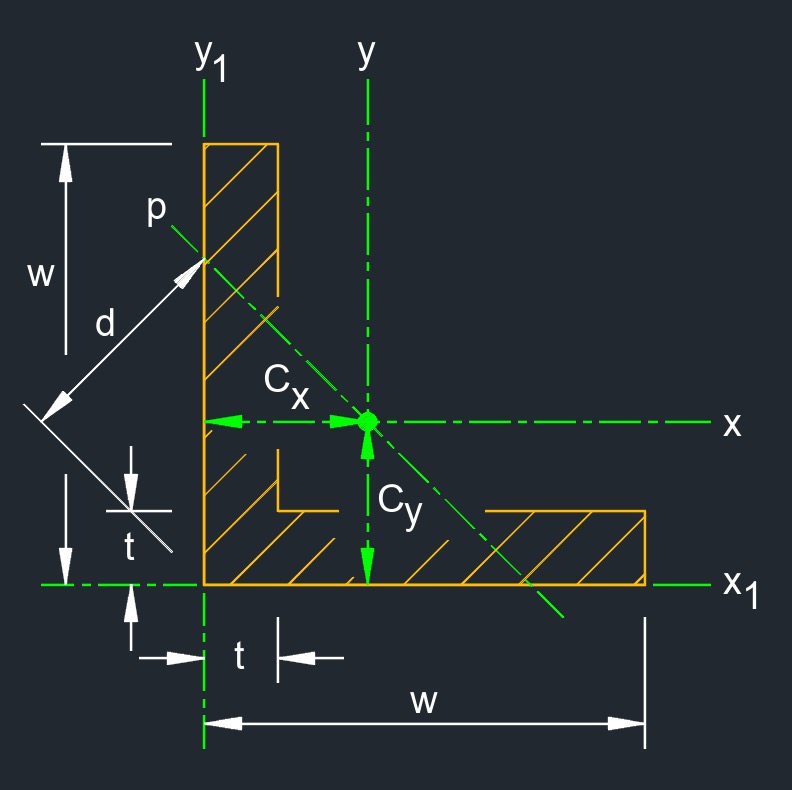Square angle is an angle iron with square legs, creating a right angle. This type of angle iron has equal length sides forming a 90-degree corner. It's commonly used as a structural component in various construction and engineering applications due to its rigidity and load-bearing capacity. Square angles, like other angle iron profiles, come in various sizes, thicknesses, and materials to accommodate different load-bearing capacities and design requirements. The cross-sectional properties of the angle, such as the moment of inertia and section modulus, determine its performance under different loading conditions.

Distance from Centroid of a Square Angle formulas
$C_x \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) }$ $C_y \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) }$
Symbol	English	Metric
$C$ = distance from centroid	$\large{ in }$	$\large{ mm }$
$t$ = thickness	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

Elastic Section Modulus of a Square Angle formulas
$S_x \;=\; \dfrac{ I_x }{ C_y }$ $S_y \;=\; \dfrac{ I_y }{ C_x }$
Symbol	English	Metric
$S$ = elastic section modulus	$\large{ in^3 }$	$\large{ mm^3 }$
$C$ = distance from centroid	$\large{ in }$	$\large{ mm }$
$I$ = moment of inertia	$\large{ in^4 }$	$\large{ mm^4 }$

Perimeter of a Square Angle formula
$P \;=\; 4\cdot w$
Symbol	English	Metric
$P$ = perimeter	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

Polar Moment of Inertia of a Square Angle formulas
$J_{z} \;=\; I_{x} + I_{y}$ $J_{z1} \;=\; I_{x1} + I_{y1}$
Symbol	English	Metric
$J$ = torsional constant	$\large{ in^4 }$	$\large{ mm^4 }$
$I$ = moment of inertia	$\large{ in^4 }$	$\large{ mm^4 }$

Principal Axis of a Square Angle formula
$d \;=\; \dfrac{ w^2 + w\cdot t - t^2 }{ 2 \cdot \left( 2\cdot w - t \right) \cdot cos( 45^\circ) }$
Symbol	English	Metric
$d$ = distance from principle axis	$\large{ in }$	$\large{ mm }$
$t$ = thickness	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

Radius of Gyration of a Square Angle formulas
$k_{x} \;=\; \sqrt{ \dfrac { I_{x} }{ A } }$ $k_{y} \;=\; \sqrt{ \dfrac { I_{y} }{ A } }$ $k_{z} \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} }$ $k_{x1} \;=\; \sqrt{ \dfrac { I_{x1} }{ A } }$ $k_{y1} \;=\; \sqrt{ \dfrac { I_{y1} }{ A } }$ $k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} }$
Symbol	English	Metric
$k$ = radius of gyration	$\large{ in }$	$\large{ mm }$
$A$ = area	$\large{ in^2 }$	$\large{ mm^2 }$
$I$ = moment of inertia	$\large{ in^4 }$	$\large{ mm^4 }$

Second Moment of Area of a Square Angle formulas
$I_{x} \;=\; \dfrac{ t \cdot \left( w - C_y \right)^3 + w \cdot \left[ w - \left( w - C_y \right) \right]^3 - \left( w - t \right) \cdot \left[ w - \left( w - C_y \right) - t \right]^3 }{3}$ $I_{x} \;=\; \dfrac{ t \cdot \left( w - C_y \right)^3 + w \cdot \left[ w - \left( w - C_y \right) \right]^3 - \left( w - t \right) \cdot \left[ w - \left( w - C_y \right) - t \right]^3 }{3}$ $I_{x1} \;=\; I_{x} + A\cdot C_{y}$ $I_{y1} \;=\; I_{y} + A\cdot C_{x}$
Symbol	English	Metric
$I$ = moment of inertia	$\large{ in^4 }$	$\large{ mm^4 }$
$A$ = area	$\large{ in^2 }$	$\large{ mm^2 }$
$C$ = distance from centroid	$\large{ in }$	$\large{ mm }$
$t$ = thickness	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

Tortional Constant of a Square Angle formula
$J \;=\; \dfrac{ \left[ w - \left( \dfrac {t}{2} \right) \right] + \left[ w - \left( \dfrac {t}{2} \right) \right] \cdot t^3 }{3}$
Symbol	English	Metric
$J$ = torsional constant	$\large{ in^4 }$	$\large{ mm^4 }$
$t$ = thickness	$\large{ in }$	$\large{ mm }$
$w$ = width	$\large{ in }$	$\large{ mm }$

Square Angle

area of a Square Channel formula

Distance from Centroid of a Square Angle formulas

Elastic Section Modulus of a Square Angle formulas

Perimeter of a Square Angle formula

Polar Moment of Inertia of a Square Angle formulas

Principal Axis of a Square Angle formula

Radius of Gyration of a Square Angle formulas

Second Moment of Area of a Square Angle formulas

Tortional Constant of a Square Angle formula

Similar Articles

Latest Articles

Login Form

Square Angle

area of a Square Channel formula

Distance from Centroid of a Square Angle formulas

Elastic Section Modulus of a Square Angle formulas

Perimeter of a Square Angle formula

Polar Moment of Inertia of a Square Angle formulas

Principal Axis of a Square Angle formula

Radius of Gyration of a Square Angle formulas

Second Moment of Area of a Square Angle formulas

Tortional Constant of a Square Angle formula

Similar Articles

Latest Articles