3 Connecting Circles
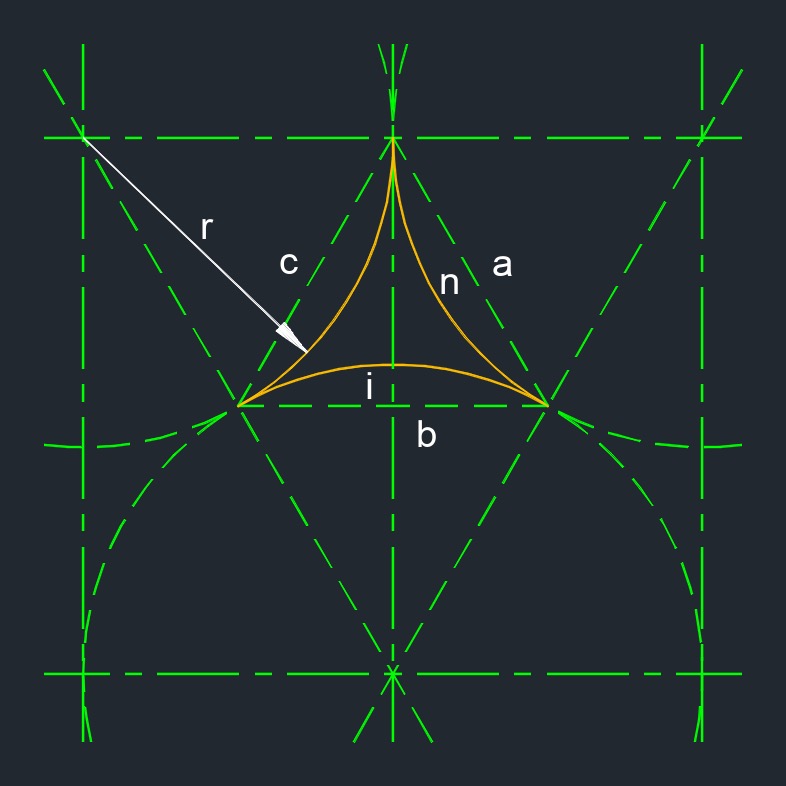- 3 connecting circles (a two-dimensional figure) has three equal length arcs connecting at the vertices bound by circles.
- a = b = c
- 3 arcs
- 3 vertexs
Arc Length of a Circle Arc Triangle formula |
||
| \( n \;=\; \frac{\pi}{3} \;r \) | ||
| Symbol | English | Metric |
| \( n \) = Arc Length | \(ft\) | \(m\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = Radius | \(ft\) | \(m\) |
Area of a Circle Arc Triangle formula |
||
| \( A_{area} \;=\; ( \sqrt{ \frac{3}{2} } + 3 ) \; ( r^2 - 3\;r\;n - 3\;r\;i ) \;/\;2 \) | ||
| Symbol | English | Metric |
| \( A_{area} \) = Area | \(ft^2\) | \(m^2\) |
| \( i \) = Arc Insert | \(ft\) | \(m\) |
| \( n \) = Arc Length | \(ft\) | \(m\) |
| \( r \) = Radius | \(ft\) | \(m\) |
Insert of a Circle Arc Triangle formula |
||
| \( i \;=\; 1 - \sqrt{ \frac{3}{2} } \; r \) | ||
| Symbol | English | Metric |
| \( i \) = Arc Insert | \(ft\) | \(m\) |
| \( r \) = Radius | \(ft\) | \(m\) |
Perimeter of a Circle Arc Triangle formula |
||
| \( P \;=\; 3\;n \) | ||
| Symbol | English | Metric |
| \( P \) = Perimeter | \(ft\) | \(m\) |
| \( n \) = Arc Length | \(ft\) | \(m\) |
Tags: Circle