Rhombus

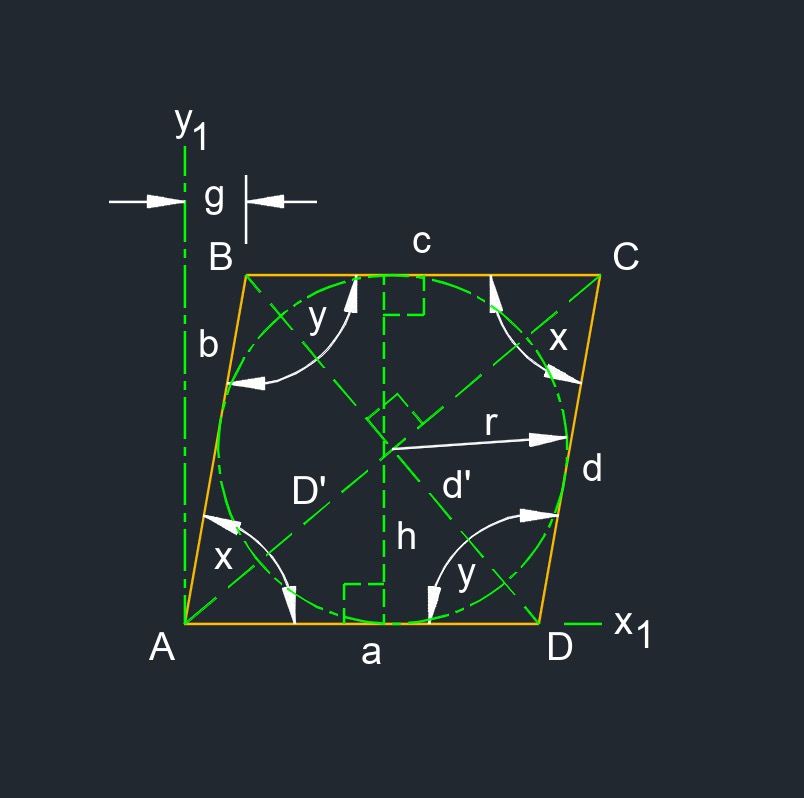• Rhombus (a two-dimensional figure) is a parallelogram with four congruent sides.
• Acute angle measures less than 90°.
• Congruent is all sides having the same lengths and angles measure the same.
• Diagonal is a line from one vertices to another that is non adjacent.
• Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
• Obtuse angle measures more than 90°.
• Parallelogram (a two-dimensional figure) is a quadrilateral with two pairs of parallel opposite sides.
• a ∥ c
• b ∥ d
• a = b = c = d
• ∠A & ∠C < 90°
• ∠B & ∠D > 90°
• ∠A + ∠B = 180°
• ∠C + ∠D = 180°
• 4 angle
• 2 diagonals
• 4 edges
• 4 vertexs

 

Angle of a Rhombus formula

\(\large{  y =  180° - x }\)

Where:

\(\large{ x }\) = acute angle

\(\large{ y }\) = obtuse angle

 

Area of a Rhombus formulas

\(\large{ A_{area} = \frac {D' \;d' } {2} }\)
\(\large{ A_{area} = h \;a }\)
\(\large{ A_{area} = a^2 \; sin\; x }\)
\(\large{ A_{area} = 2\; a\; r }\)
\(\large{ A_{area} = \frac{4\; r^2}{sin\;x} }\)

Where:

\(\large{ A_{area} }\) = area

\(\large{ d', D' }\) = diagonal

\(\large{ a, b, c, d }\) = edge

\(\large{ r }\) = inside radius

\(\large{ x }\) = acute angle

\(\large{ y }\) = obtuse angle

 

Angle of a Rhombus formulas

\(\large{ sin \; x =  \frac {2\;D'\;d'}{D'^2 \;+\; d'^2}  }\)
\(\large{ sin \; y =  \frac {2\;D'\;d'}{D'^2 \;+\; d'^2}  }\)
\(\large{ cos \; x = 1 - \frac {d'^2}{2\; a^2}  }\)
\(\large{ cos \; x = \frac {D'^2}{2\; a^2} - 1 }\)
\(\large{ cos \; y = 1 - \frac {D'^2}{2\; a^2}  }\)
\(\large{ cos \; y = \frac {d'^2}{2\; a^2} - 1 }\)
\(\large{ sin \; x =  \frac {A}{a^2 }  }\)
\(\large{ sin \; y =  \frac {A}{a^2 }  }\)

Where:

\(\large{ x }\) = acute angle

\(\large{ y }\) = obtuse angle

\(\large{ A_{area} }\) = area

\(\large{ d',\; D' }\) = diagonal

\(\large{ a, b, c, d }\) = edge

 

Diagonal of a Rhombus formulas

\(\large{ d' = \frac {2\;A_{area}}{D'} }\)
\(\large{ D' = \frac {2\;A_{area}}{d'} }\)
\(\large{ d' =  \sqrt{  4\;a^2 - D'^2  }   }\)
\(\large{ D' =  \sqrt{  4\;a^2 - d'^2  }   }\)
\(\large{ d' = a  \sqrt{  2 - 2 \; cos \; x }   }\)
\(\large{ d' = a  \sqrt{  2+ 2 \; cos \; y }   }\)
\(\large{ D' = a  \sqrt{  2 - 2 \; cos \; y }   }\)
\(\large{ D' = a  \sqrt{  2 + 2 \; cos \; x }   }\)
\(\large{ d' = 2\;a \; cos \left(  \frac{y}{ 2} \right)    }\)
\(\large{ d' = 2\;a \; sin \left(  \frac{x}{ 2} \right)    }\)
\(\large{ D' = 2\;a \; cos \left(  \frac{x}{ 2} \right)    }\)
\(\large{ D' = 2\;a \; sin \left(  \frac{y}{ 2} \right)    }\)

Where:

\(\large{ d', D' }\) = diagonal

\(\large{ A_{area} }\) = area

\(\large{ a, b, c, d }\) = edge

\(\large{ x }\) = acute angle

\(\large{ y }\) = obtuse angle

 

Edge of a Rhombus formulas

\(\large{ a = \frac {P} {4} }\)
\(\large{ a = \frac { \sqrt { {D'}^2 \;+\; {D'}^2 } } { 2 }   }\)
\(\large{ a =   \sqrt{  \frac{ A }{ sin\;x }  }   }\)
\(\large{ a =   \sqrt{  \frac{ A }{ sin\;y }  }   }\)
\(\large{ a = \frac {d'} { \sqrt{ 2 \;-\; 2 \; cos\; x }    }  }\)
\(\large{ a = \frac {d'} { \sqrt{ 2 \;+\; 2 \; cos\; y }    }  }\)
\(\large{ a = \frac {D'} { \sqrt{ 2 \;-\; 2 \; cos\; y }    }  }\)
\(\large{ a = \frac {D'} { \sqrt{ 2 \;+\; 2 \; cos\; x }    }  }\)
\(\large{ a =   \sqrt{  \frac{ D' \; d' }{ 2 \; sin \; x }  }   }\)
\(\large{ a =   \sqrt{  \frac{ D' \; d' }{ 2 \; sin \; y }  }   }\)

Where:

\(\large{ a, b, c, d }\) = edge

\(\large{ A_{area} }\) = area

\(\large{ d',\; D' }\) = diagonal

\(\large{ P }\) = perimeter

\(\large{ x }\) = acute angle

\(\large{ y }\) = obtuse angle

 

Inscribed Circle Radius of a Rhombus formulas

\(\large{ r = \frac{h}{2}   }\)
\(\large{ r = \frac{A_{area}}{2 a}   }\)
\(\large{ r = \frac{D' \; d'}{4 a}   }\)
\(\large{ r = \frac{ \sqrt{A_{area}\;sin\;x } }{2}   }\)
\(\large{ r = \frac{a\;sin\;x}{2}   }\)
\(\large{ r = \frac{a\;sin\;y}{2}   }\)
\(\large{ r = \frac{ D'\;sin \frac{x}{2}  }{2}   }\)
\(\large{ r = \frac{ d'\;sin \frac{y}{2}  }{2}   }\)
\(\large{ r = \frac{ D'\; d' }{ 2\;\sqrt{ D'^2 \;+\; d'^2 } }   }\)

Where:

\(\large{ r }\) = inside radius

\(\large{ A_{area} }\) = area

\(\large{ d',\; D' }\) = diagonal

\(\large{ h }\) = hight

\(\large{ a, b, c, d }\) = edge

 

Perimeter of a Rhombus formulas

\(\large{ P = 4\;a }\)

Where:

\(\large{ P }\) = perimeter

\(\large{ a, b, c, d }\) = edge