Skip to main content

Annulus of a Circle

Tags:
Circle

Area of an Annulus formulas
$A \;=\; \pi \cdot r^2 - \pi \cdot R^2$ $A \;=\; \pi \cdot ( r^2 - R^2 )$
Symbol	English	Metric
$A$ = area	$in^2$	$mm^2$
$r$ = inside radius	$in$	$mm$
$R$ = outside radius	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

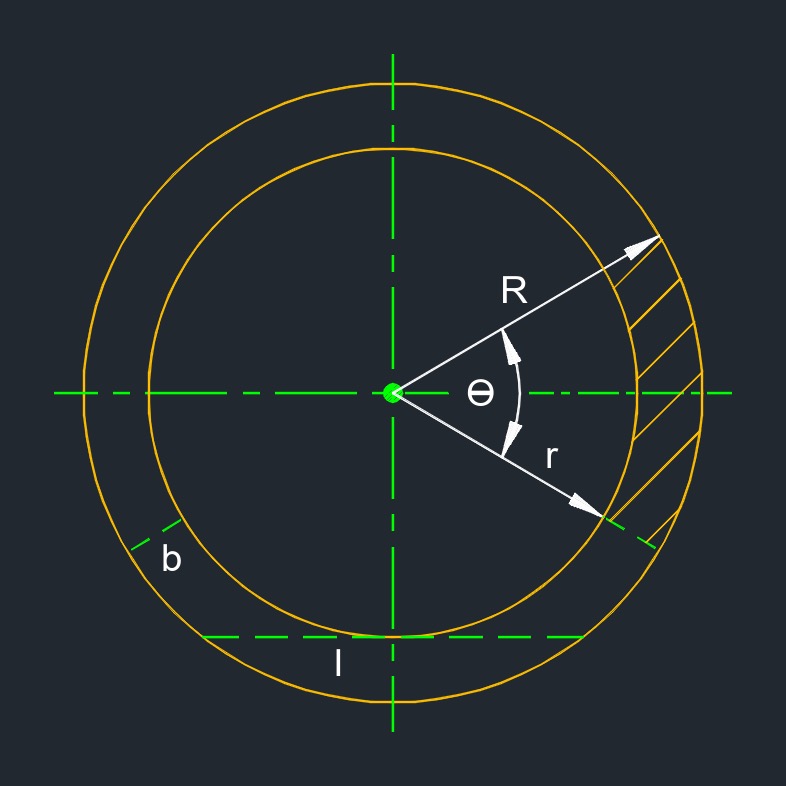The area between two concentric circles.

Inside Radius of an Annulus formula
$r \;=\; \sqrt{ R^2 - \dfrac{ A }{ \pi } }$
Symbol	English	Metric
$r$ = inside radius	$in$	$mm$
$A$ = area	$in^2$	$mm^2$
$R$ = outside radius	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

Outside Radius of an Annulus formula
$R \;=\; \sqrt{ r^2 - \dfrac{ A }{ \pi } }$
Symbol	English	Metric
$R$ = outside radius	$in$	$mm$
$A$ = area	$in^2$	$mm^2$
$r$ = inside radius	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

Area of a sector of an Annulus formula
$A \;=\; \dfrac{ \pi \cdot \theta }{ 360^{\circ} } \cdot ( R^2 - r^2 )$
Symbol	English	Metric
$A$ = area	$in^2$	$mm^2$
$\theta$ = degree	$deg$	$rad$
$r$ = inside radius	$in$	$mm$
$R$ = outside radius	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

Breadth of an Annulus formula
$b \;=\; R - r$
Symbol	English	Metric
$b$ = breadth	$in$	$mm$
$r$ = inside radius	$in$	$mm$
$R$ = outside radius	$in$	$mm$

Longest Interval of an Annulus formula
$l \;=\; 2 \cdot \sqrt{ R^2 - r^2 }$
Symbol	English	Metric
$l$ = longest interval	$in$	$mm$
$r$ = inside radius	$in$	$mm$
$R$ = outside radius	$in$	$mm$

Perimeter of an Annulus formula
$P \;=\; 2 \cdot \pi \cdot ( R + r )$
Symbol	English	Metric
$P$ = perimeter	$in$	$mm$
$r$ = inside radius	$in$	$mm$
$R$ = outside radius	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

Similar Articles

Latest Articles