Average Angular Velocity Change in Velocity Formulas |
||
|
\( \bar {\omega} \;=\; \dfrac{ \omega_t }{ t_t }\) \( \bar {\omega} \;=\; \dfrac{ \omega_1 + \omega_2 + \omega_3 ... \omega_n }{ t_1 + t_2 + t_3 ... t_n }\) |
||
| Symbol | English | Metric |
| \( \bar {\omega} \) (Greek symbol omega) = average angular velocity | \(deg \;/\; sec\) | \(rad \;/\; s\) |
| \( \omega \) (Greek symbol omega) = angular velocity | \(deg \;/\; sec\) | \(rad \;/\; s\) |
| \( t \) = time | \( sec \) | \( s \) |
| \( \omega_t \) (Greek symbol omega) = total angular velocity | \(deg \;/\; sec\) | \(rad \;/\; s\) |
| \( t_t \) = total time | \( sec \) | \( s \) |
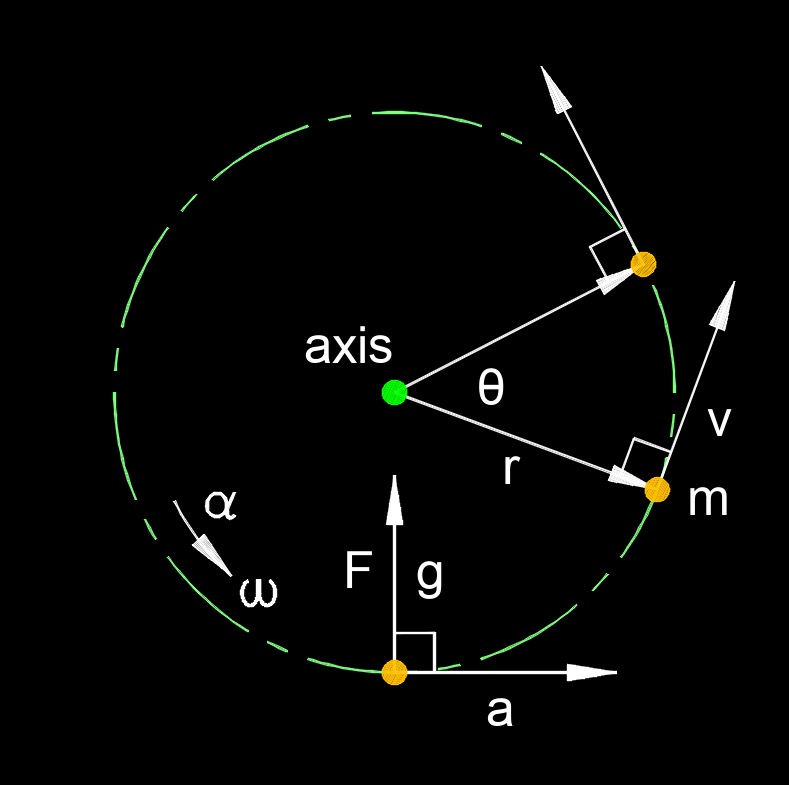When an object makes changes in its angular velocity at different times that is an average angular velocity of any given velocities.
