Moment of Inertia of a Mass Formula, Single Mass |
||
| \( I \;=\; m \cdot r^2 \) | ||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \(lbm\;/\;ft^2-sec\) | \(kg\;/\;m^2\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( r \) = Radius | \(ft\) | \(m\) |
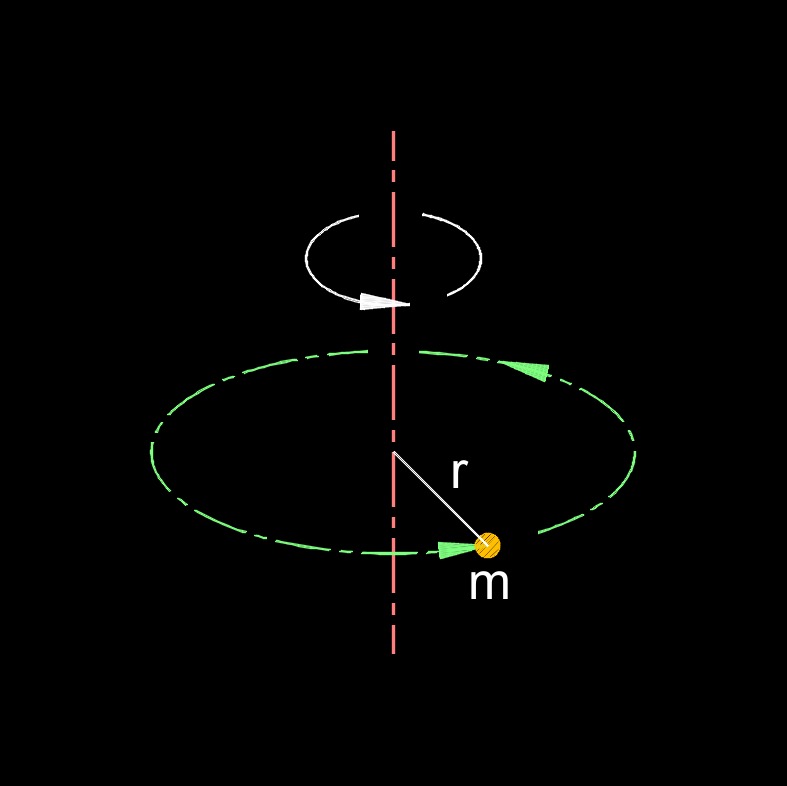
Moment of inertia of a mass, abbreviated as I, is a measure of how an object's mass is distributed in relation to a specific axis of rotation. It quantifies an object's resistance to changes in its rotational motion. In other words, it tells you how difficult or easy it is to make an object rotate about a particular axis. For more complex objects with extended shapes and continuous mass distributions, the moment of inertia can be calculated through integration or using specific formulas for common shapes like cylinders, spheres, rods, and so on.
Moment of Inertia of a Mass Formula, Multiple Masses |
||
| \( I \;=\; m_1 \cdot r_1{^2} + m_2 \cdot r_2{^2} + m_3 \cdot r_3{^2} \) | ||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \(lbm\;/\;ft^2-sec\) | \(kg\;/\;m^2\) |
| \( m_1 \) = Mass | \(lbm\) | \(kg\) |
| \( m_2 \) = Mass | \(lbm\) | \(kg\) |
| \( m_3 \) = Mass | \(lbm\) | \(kg\) |
| \( r_1 \) = Radius | \(ft\) | \(m\) |
| \( r_2 \) = Radius | \(ft\) | \(m\) |
| \( r_3 \) = Radius | \(ft\) | \(m\) |
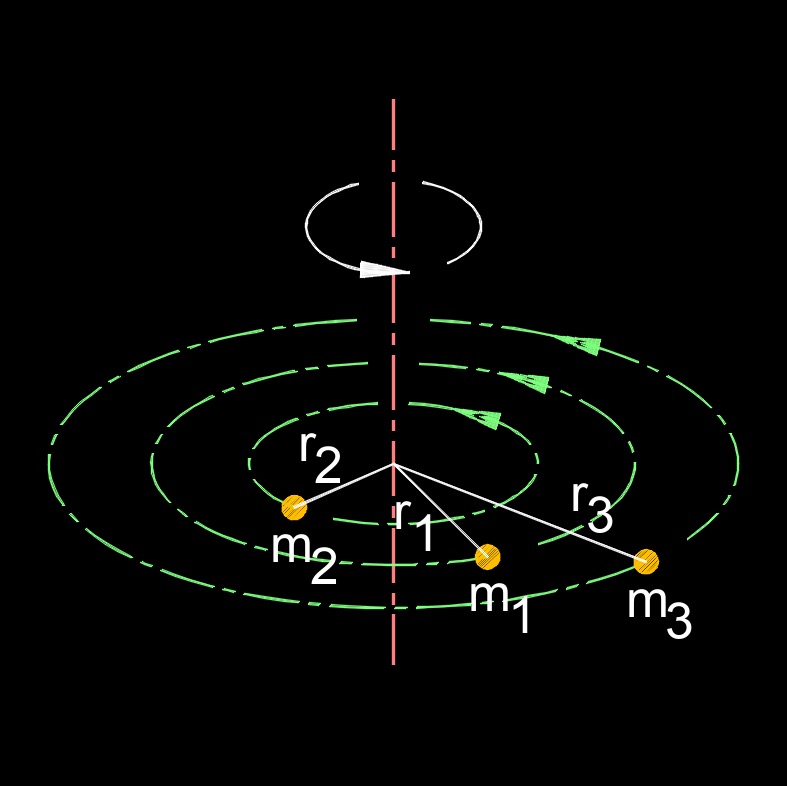In engineering and physics, understanding the moment of inertia is crucial when analyzing the behavior of rotating objects, such as wheels, gears, or any object subject to angular acceleration or deceleration. It helps in predicting how these objects will respond to external torques and how they will resist changes in their rotational motion.
