Angular Displacement Formula |
||
|
\( \theta_d \;=\; \dfrac{ s }{ r }\) (Angular Displacement) \( s \;=\; \theta_d \cdot r \) \( r \;=\; \dfrac{ s }{ \theta_d }\) |
||
| Symbol | English | Metric |
| \( \theta_d \) (Greek symbol theta) = Angular Displacement | \(deg\) | \(rad\) |
| \( s \) = Distance Covered by the Object on the Circular Path | \(ft\) | \(m\) |
| \( r \) = Circular Path Radius | \(ft\) | \(m\) |
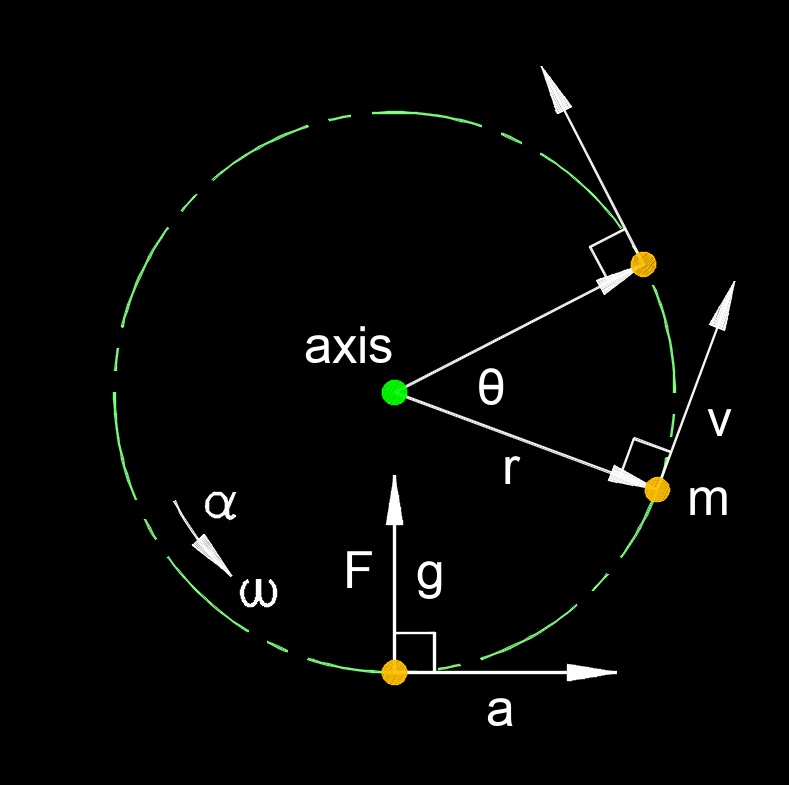Angular displacement, abbreviated as \( \theta \) (Greek symbol theta), is the angle through which a body moves in a circular path. It is the change in the orientation or angular position of an object relative to a reference point or axis. It is a measure of the angle through which an object has rotated or turned from its initial position to its final position. Angular displacement can be either positive or negative, depending on the direction of rotation. Conventionally, counterclockwise rotations are considered positive, while clockwise rotations are considered negative.
Angular Displacement from Angular Velocity Formula |
||
|
\( \theta_d \;=\; \omega \cdot t \) (Angular Displacement from Angular Velocity) \( \omega \;=\; \dfrac{ \theta_d }{ t }\) \( t \;=\; \dfrac{ \theta_d }{ \omega }\) |
||
| Symbol | English | Metric |
| \(\theta_d \) (Greek symbol theta) = Angular Displacement | \(deg\) | \(rad\) |
| \( \omega \) (Greek symbol omega) = Angular Velocity | \(\deg \;/\; sec\) | \(rad \;/\; s\) |
| \( t \) = Time | \(sec\) | \(s\) |
Angular displacement is a concept in rotational dynamics and is used to describe the motion of objects undergoing rotational or circular motion. It is closely related to other rotational quantities, such as angular velocity and angular acceleration. Angular displacement is particularly useful for understanding the motion of rotating objects, such as wheels, gears, and pendulums. It is also applicable in various fields, including physics, engineering, and astronomy, where angular measurements and rotational motion analysis are required.
It's important to note that angular displacement differs from linear displacement, which measures the change in position along a straight line. Angular displacement, on the other hand, quantifies the change in orientation or angle.
