Trajectory of a Projectile on a Hill formulas |
||
|
\( t \;=\; \dfrac{ 2 \cdot v_{0h} }{ g } \pm \sqrt{ \dfrac{ v_{0h}^2 }{ g^2 } - \dfrac{ 2 \cdot h }{ g } } \) \( d \;=\; v_{0d} \cdot t \) \( h \;=\; v_{0h} \cdot t - \dfrac{1}{2} \cdot g \cdot t^2 \) |
||
| Symbol | English | Metric |
| \( t \) = time | \(sec\) | \(s\) |
| \( g \) = gravitational acceleration | \(ft\;/\;sec^2\) | \(m\;/\;s^2\) |
| \( v_0 \) = launch velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( \theta \) = vertical angle | \(rad\) | \(rad\) |
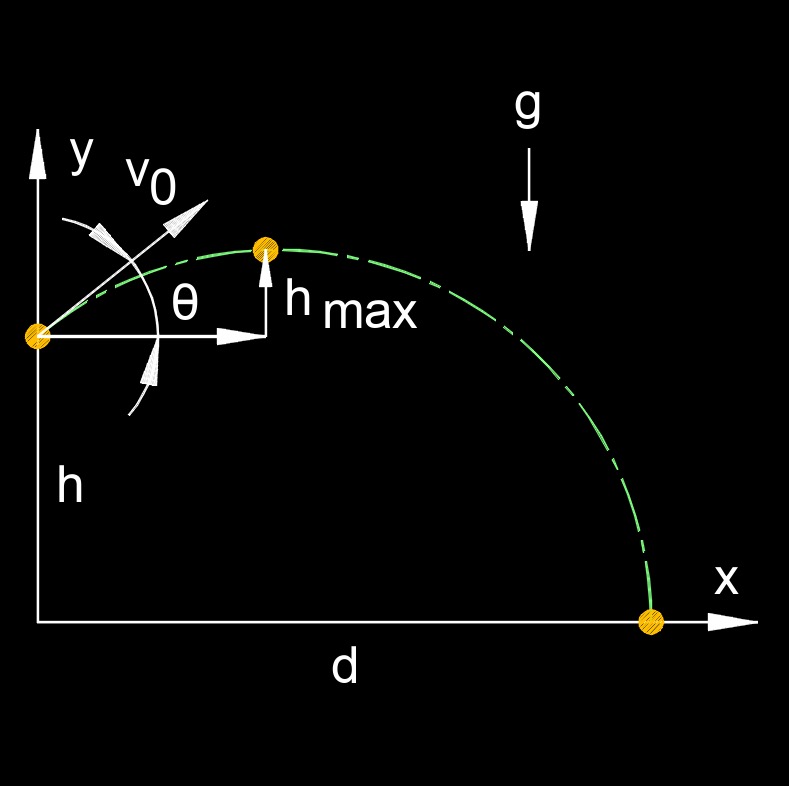Trajectory of a projectile on a hill introduces some extra complexity compared to the flat-ground case, because the "ground" itself is no longer level, it’s inclined. This affects the projectile’s path, range, and landing point, since the hill’s slope changes the reference plane and the conditions for where the projectile stops. Let’s break it down step-by-step.
- Trajectory - A projectile’s path under gravity (no air resistance) is a parabola when launched from a flat surface. Its motion is governed by initial velocity, launch angle, and gravity.
- Hills Influence - When the launch point is on a hill with an incline angle (say, positive for uphill), the ground slopes, so the projectile’s trajectory must be analyzed relative to this tilted surface. The effective launch angle relative to the horizontal. The point where the projectile lands, since the ground rises or falls along the slope.
