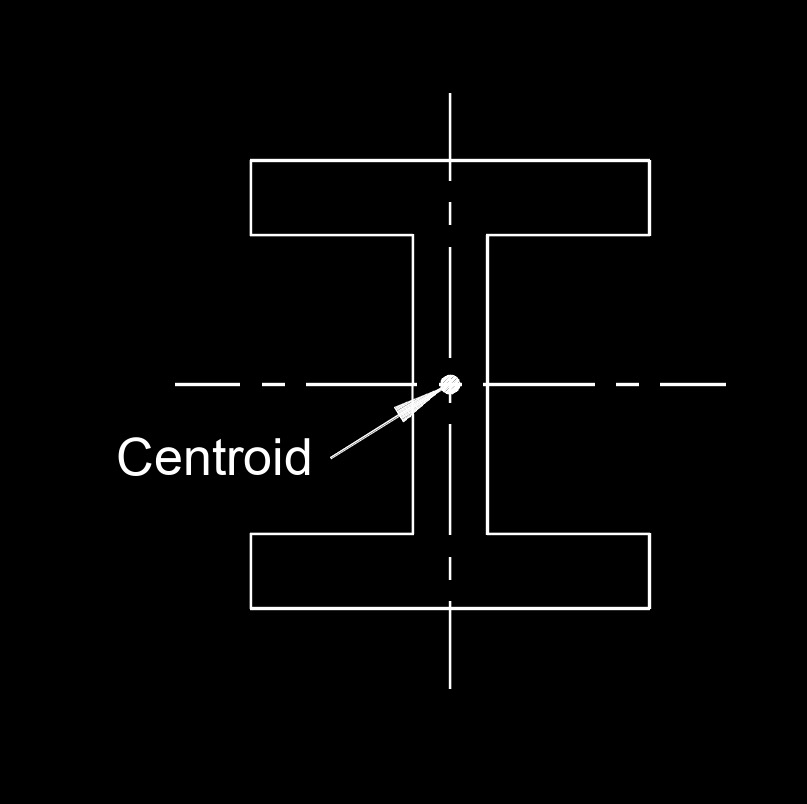
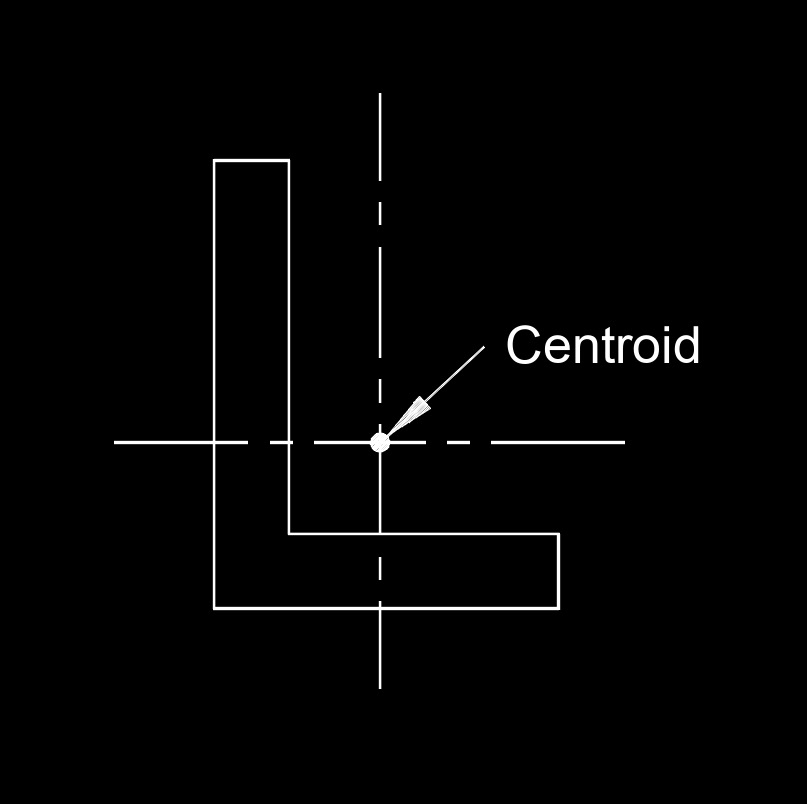
Centroid is a geometric concept that represents the center or the average position of a set of points in a space. The specific definition of a centroid can vary depending on the context in which it is used. In geometry, a geometric centroid in a two-dimensional shape (like a triangle or a polygon) is the point at which all the individual points of the shape would balance if it were cut out of a uniform material. For example, in a triangle, the centroid is the point where the medians intersect. In physics, the term centroid can refer to the center of mass or center of gravity of an object. It is the point at which the entire mass of an object can be considered to be concentrated for the purposes of calculating its response to external forces.
Centroid Common Interpretations
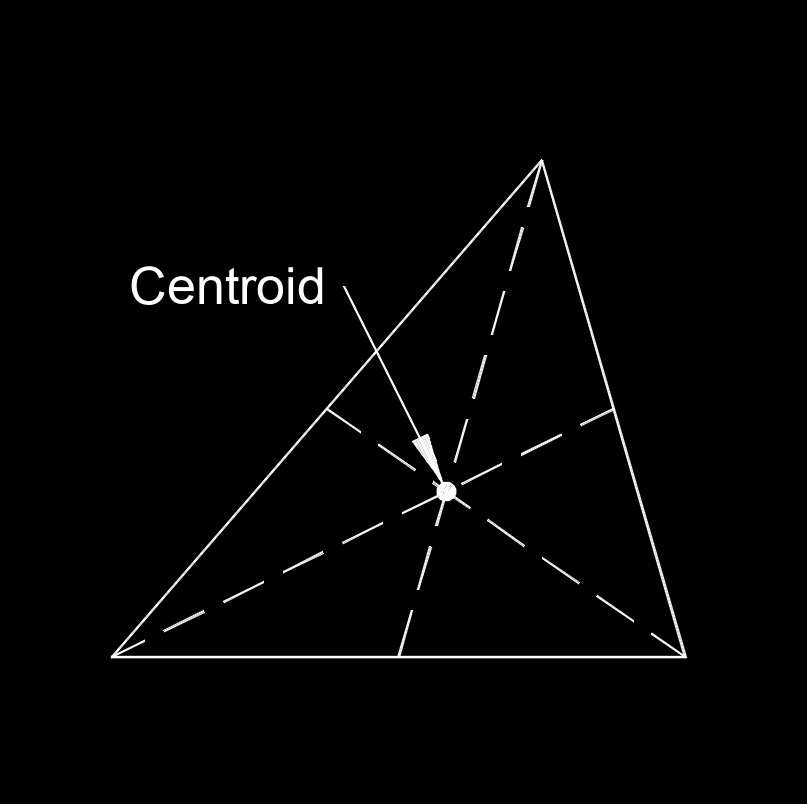
Geometric Centroid - In geometry, the centroid of a two-dimensional shape (like a triangle or a polygon) is the point at which all the individual points of the shape would balance if it were cut out of a uniform material. For example, in a triangle, the centroid is the point where the medians (lines connecting a vertex to the midpoint of the opposite side) intersect.
Centroid in Statistics - In statistics, a centroid is often used to represent the average of a set of data points. For instance, in multivariate analysis, the centroid of a cluster of data points is the mean (average) of each variable's value for all the points in that cluster.
Centroid in Physics - In physics, the term centroid can refer to the center of mass or center of gravity of an object. It is the point at which the entire mass of an object can be considered to be concentrated for the purposes of calculating its response to external forces.
Centroid in Computer Science - In computer science and image processing, the centroid of an object or a region in an image is often used for various purposes, including object tracking, shape analysis, and image recognition. It is calculated as the weighted average of the pixel positions within the object or region.
The concept of a centroid is versatile and can be applied in various fields to represent a central or average position, whether in geometry, statistics, physics, or computer science. The specific method for calculating a centroid may differ depending on the context and the type of data or objects involved.





