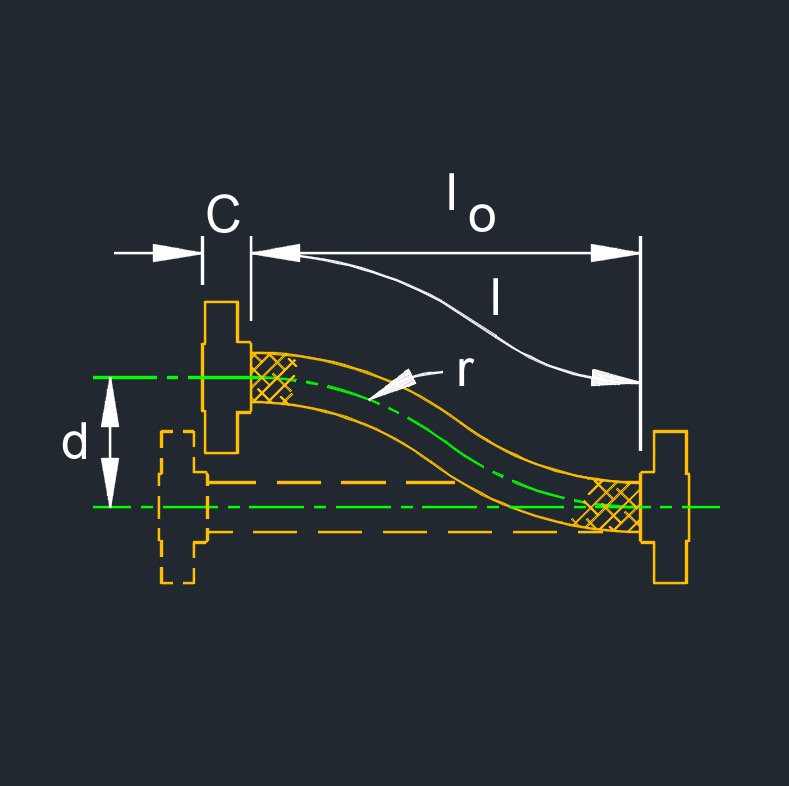
Lateral Deflection Hose Length Formula |
||
| \( l \;=\; \sqrt{ 6 \cdot r \cdot d + d^2 } \) | ||
| Symbol | English | Metric |
| \( l \) = hose length | \(ft\) | \(m\) |
| \( r \) = minimum centerline bend radius for constant flexing | \(ft\) | \(m\) |
| \( d \) = offset distance from centerline | \(ft\) | \(m\) |
Lateral deflection is the horizontal displacement or bending of a structure or object when subjected to external forces or loads. It is a measure of how much a component or system moves sideways from its original position under the influence of lateral forces.
Lateral Deflection Offset Hose Length Formula |
||
| \( l_o \;=\; \sqrt{ l^2 - d^2 } \) | ||
| Symbol | English | Metric |
| \( l_o \) = offset hose length | \(ft\) | \(m\) |
| \( l \) = hose length | \(ft\) | \(m\) |
| \( d \) = offset distance from centerline | \(ft\) | \(m\) |
In engineering and mechanics, lateral deflection is an essential consideration for designing and analyzing various structures, such as beams, columns, bridges, and other load-bearing elements. When subjected to lateral loads, such as wind, earthquake, or applied forces, structures can experience lateral deflection, which can influence their overall stability and performance.
The amount of lateral deflection depends on several factors, including the material properties of the structure, the magnitude and direction of the applied forces, the shape and geometry of the component, and the support conditions. Engineers aim to control and limit lateral deflection within acceptable limits to ensure the safety and functionality of the structure. Engineers use various techniques to mitigate lateral deflection, such as adding diagonal bracing, increasing the stiffness of materials, or incorporating additional supports to enhance the overall stability of the structure.
