Darcy's Law Formula
|
||
| \( Q \;=\; - k \cdot A_c \cdot \dfrac{ \Delta h }{ l }\) | ||
| Symbol | English | Metric |
| \( Q \) = Volumetric Flow Rate of the Fluid Through the Porous Medium | \(ft^3 \;/\; sec\) | \(m^3 \;/\; s\) |
| \( k \) = Hydraulic Conductivity of the Porus Media | \(ft \;/\; day\) | \(m \;/\; day\) |
| \( A_c \) = Area Cross-section Perpendicular to the Flow | \(ft^2\) | \(m^2\) |
| \( \Delta h \) = Hydraulic Head Along the Flow Path | \(ft\) | \(m\) |
| \( l \) = Length of Flow Path | \(ft\) | \(m\) |
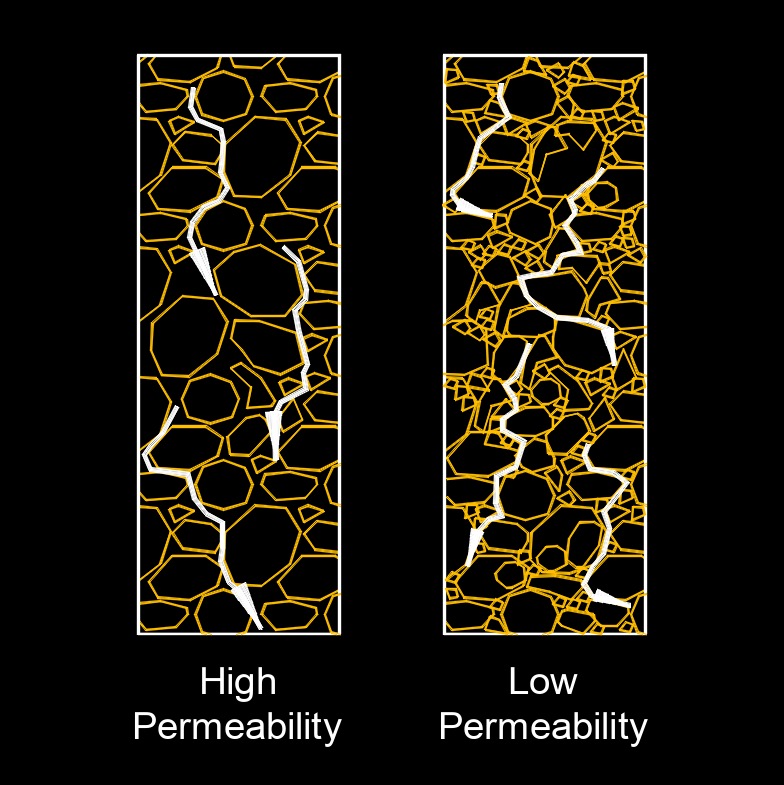Darcy's law, abbreviated as Da, describing the rate at which a fluid flows through a permeable medium. The law states that this rate is directly proportional to the drop in vertical elevation between two places in the medium and indirectly proportional to the distance between them. The law is used to describe the flow of water from one part of an aquifer to another and the flow of petroleum through sandstone and gravel. Darcy's law describes how fluids move through porous materials in response to a pressure gradient.
Darcy's law assumes that the flow is laminar, the fluid is incompressible, and the porous medium is homogeneous and isotropic. It provides a simplified representation of fluid flow through porous media and forms the basis for more complex models and equations used in hydrogeology and reservoir engineering.
