Continuity Equation

Continuity Equation for Area Formula This formula calculates the initial cross-section area of the pipe.
\( A_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ v_1 \cdot \rho_1 }\) (Continuity Equation for Area) \( \rho_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ A_2 \cdot v_2 }\) \( A_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ \rho_2 \cdot v_2 }\) \( v_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ \rho_2 \cdot A_2 }\) \( v_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot \rho_1 }\) \( \rho_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot v_1 }\)
Symbol	English	Metric
\( A_1 \) = Initial Area Cross-section	\(in^2\)	\(mm^2\)
\( \rho_2 \) (Greek symbol rho) = Final Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)
\( A_2 \) = Final Area Cross-section	\(in^2\)	\(mm^2\)
\( v_2 \) = Final Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( v_1 \) = Initial Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( \rho_1 \) (Greek symbol rho) = Initial Area Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)

The continuity equation, also called conservation of mass equation, is a fundamental principle in fluid dynamics that describes the conservation of mass within a fluid flow. It states that the rate of change of mass within a control volume is equal to the net rate of mass flow into or out of the control volume. The continuity equation can also be stated that the change in density over time in a given region is equal to the negative divergence of the mass flux density. This equation implies that mass is conserved, meaning that the amount of fluid entering or leaving a control volume must be balanced by the change in mass within that volume.

The continuity equation is widely applied in various fields of fluid dynamics, including hydrodynamics, aerodynamics, and fluid flow analysis. It is a fundamental equation used in conjunction with other equations, such as the Navier-Stokes equations, to analyze and solve fluid flow problems.

Continuity Equation for Density Formula This formula calculates the initial density of the fluid.
\( \rho_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot v_1 }\) (Continuity Equation for Density) \( \rho_2 \;=\; \dfrac{ \rho_1 \cdot A_1 \cdot v_1 }{ A_2 \cdot v_2 }\) \( A_2 \;=\; \dfrac{ \rho_1 \cdot A_1 \cdot v_1 }{ \rho_2 \cdot v_2 }\) \( v_2 \;=\; \dfrac{ \rho_1 \cdot A_1 \cdot v_1 }{ \rho_2 \cdot A_2 }\) \( A_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ \rho_1 \cdot v_1 }\) \( v_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ \rho_1 \cdot A_1 }\)
Symbol	English	Metric
\( \rho_1 \) (Greek symbol rho) = Initial Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)
\( \rho_2 \) (Greek symbol rho) = Final Area Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)
\( A_2 \) = Final Area Cross-section	\(in^2\)	\(mm^2\)
\( v_2 \) = Final Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( A_1 \) = Initial Area Cross-section	\(in^2\)	\(mm^2\)
\( v_1 \) = Initial Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)

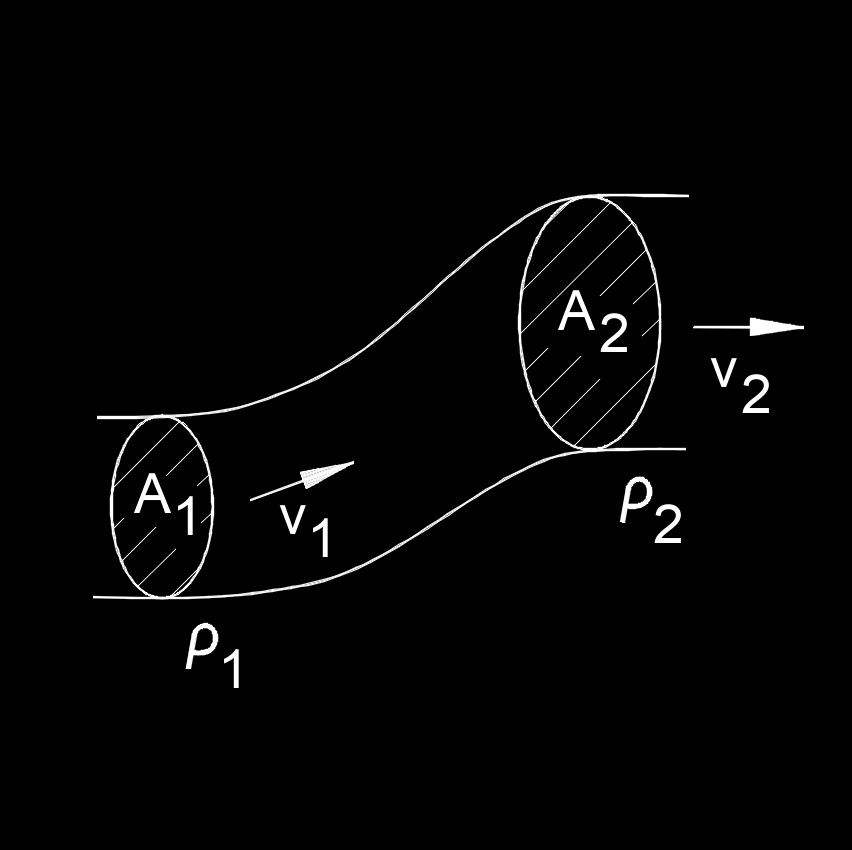
Continuity Equation for Mass Formula This formula states that the mass entering a system is equal to the mass leaves the system both at the same rate.
\( A_1 \cdot v_1 \;=\; A_2 \cdot v_2 \) (Continuity Equation for Mass) \( A_1 \;=\; \dfrac{ A_2 \cdot v_2 }{ v_1 }\) \( v_1 \;=\; \dfrac{ A_2 \cdot v_2 }{ A_1 }\) \( A_2 \;=\; \dfrac{ A_1 \cdot v_1 }{ v_2 }\) \( v_2 \;=\; \dfrac{ A_1 \cdot v_1 }{ A_2 }\)
Symbol	English	Metric
\( A_1 \) = Initial Area Cross-section	\(in^2\)	\(mm^2\)
\( v_1 \) = Initial Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( A_2 \) = Final Area cross-section	\(in^2\)	\(mm^2\)
\( v_2 \) = Final Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)

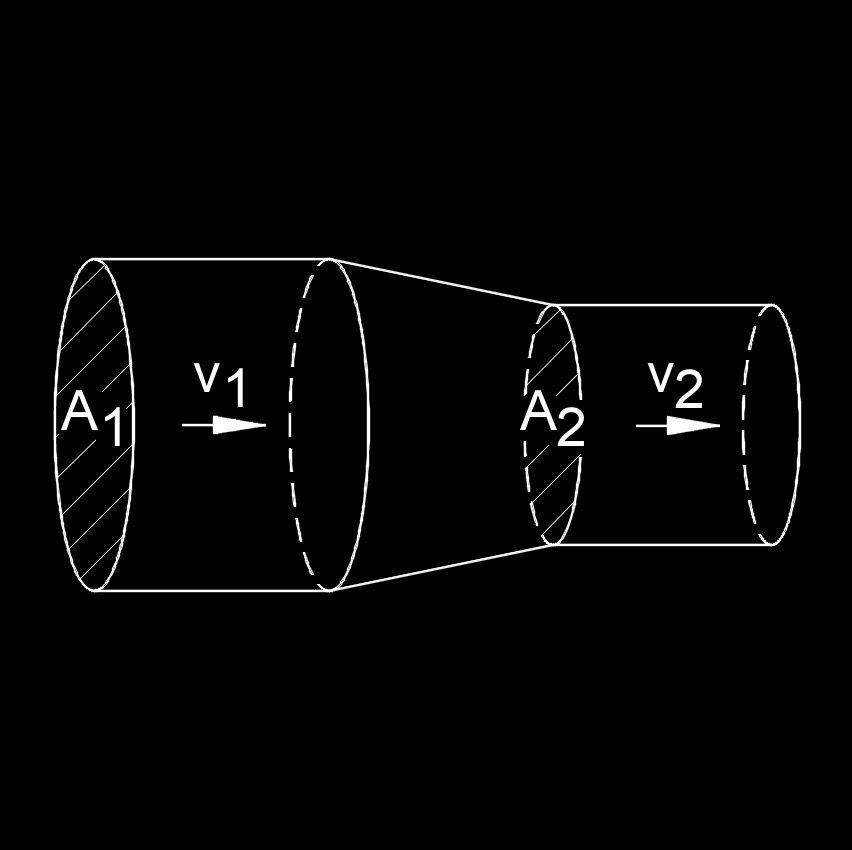
Continuity Equation for Velocity Formula This formula calculates the initial velocity in a pipe.
\( v_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot \rho_1 }\) (Continuity Equation for Velocity) \( \rho_2 \;=\; \dfrac{ v_1 \cdot A_1 \cdot \rho_1 }{ A_2 \cdot v_2 }\) \( A_2 \;=\; \dfrac{ v_1 \cdot A_1 \cdot \rho_1 }{ \rho_2 \cdot v_2 }\) \( v_2 \;=\; \dfrac{ v_1 \cdot A_1 \cdot \rho_1 }{ \rho_2 \cdot A_2 }\) \( A_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ v_1 \cdot \rho_1 }\) \( \rho_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ v_1 \cdot A_1 }\)
Symbol	English	Metric
\(\ v_1 \) = Initial Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( \rho_2 \) (Greek symbol rho) = Final Area Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)
\( A_2 \) = Final Area Cross-section	\(in^2\)	\(mm^2\)
\( v_2 \) = Final Area Cross-section Velocity	\(ft \;/\; sec\)	\(m \;/\; s\)
\( A_1 \) = Initial Area Cross-section	\(in^2\)	\(mm^2\)
\( \rho_1 \) (Greek symbol rho) = Initial Area Cross-section Density	\(lbm \;/\; ft^3\)	\(kg \;/\; m^3\)