Mass Flow Rate
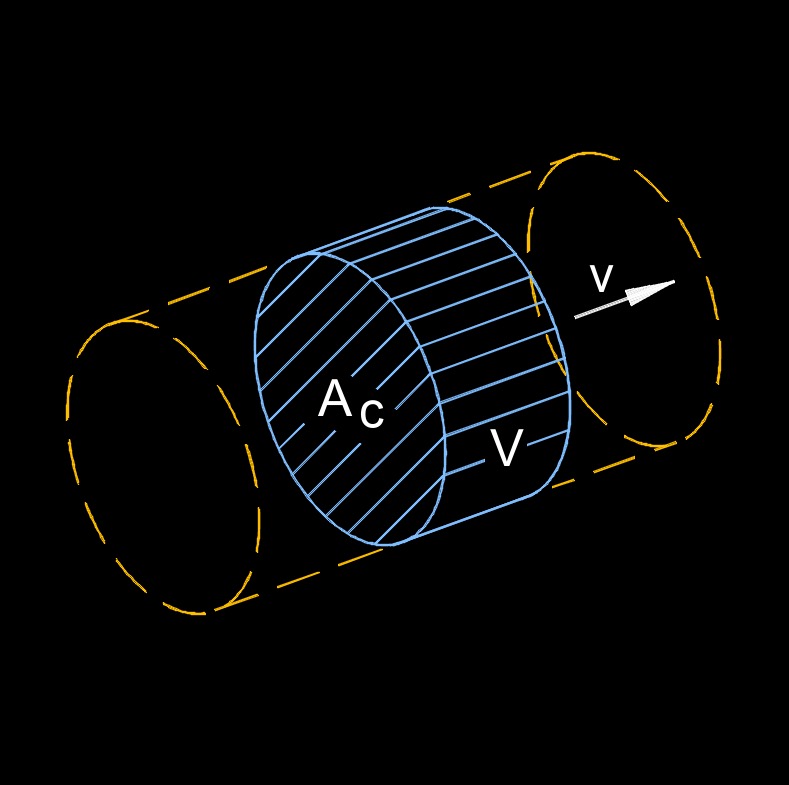Mass flow rate, abbreviated as \(\dot m_f\), is the average velocity of a mass that passes by a point. In engineering, mass flow rate is often used, along with the conservation of mass to determine how much product moves through a pipe or duct.
Mass flow rate refers to the amount of mass that passes through a given area cross-section per unit of time. It represents the rate at which mass is transported or flowing in a fluid system, such as a pipe, channel, or duct. The equation shows that the mass flow rate depends on the product density, cross-sectional area, and velocity of the fluid. A larger area or higher velocity will result in a greater mass flow rate.
In practical applications, the mass flow rate is often used to characterize the flow of fluids in various engineering and industrial processes. It is important in areas such as fluid dynamics, heat transfer, and chemical engineering, where understanding and controlling the mass flow rate of fluids is crucial for designing and optimizing systems.
Mass Flow Rate formula |
||
| \(\large{ \dot m_f = \rho \; v \; A_c }\) | ||
Mass Flow Rate - Solve for mf\(\large{ \dot m_f = \rho \; v \; A_c }\)
Mass Flow Rate - Solve for ρ\(\large{ \rho = \frac{ \dot m_f }{ v \; A_c} }\)
Mass Flow Rate - Solve for v\(\large{ v = \frac{ \dot m_f }{ \rho \; A_c} }\)
Mass Flow Rate - Solve for Ac\(\large{ A_c = \frac{ \dot m_f }{ \rho \; v } }\)
|
||
| Symbol | English | Metric |
| \(\large{ \dot m_f }\) = mass flow rate | \(\large{\frac{lbm}{sec}}\) | \(\large{\frac{kg}{s}}\) |
| \(\large{ \rho }\) (Greek symbol rho) = density of the fluid | \(\large{\frac{lbm}{ft^3}}\) | \(\large{\frac{kg}{m^3}}\) |
| \(\large{ v }\) = velocity of the fluid | \(\large{\frac{ft}{sec}}\) | \(\large{\frac{m}{s}}\) |
| \(\large{ A_c }\) = area cross-section | \(\large{ft^2}\) | \(\large{m^2}\) |
Tags: Flow Equations Mass Equations Pipeline Pigging Equations