Heat Transfer Formula |
||
|
\( q \;=\; m \cdot c \cdot \Delta T \) (Heat Transfer) \( m \;=\; \dfrac{ q }{ c \cdot \Delta T }\) \( c \;=\; \dfrac{ q }{ m \cdot \Delta T }\) \( \Delta T \;=\; \dfrac{ q }{ m \cdot c }\) |
||
| Symbol | English | Metric |
| \( q \) = Heat Transfer | \(Btu \;/\; hr\) | \(W\) |
| \( m \) = Object Mass | \(lbm\) | \(kg\) |
| \( c \) = Specific Heat | \(Btu \;/\; lbm-F\) | \(kJ \;/\; kg-K\) |
| \( \Delta T \) = Temperature Change | \( F \) | \( K \) |
Heat transfer, abbreviated as Q, is the process of exchanging thermal energy between physical systems. It is the process of thermal energy exchange between systems or objects due to a temperature difference. It is essential for understanding the behavior of materials and systems under different thermal conditions, and for designing efficient heat exchangers and thermal management systems.
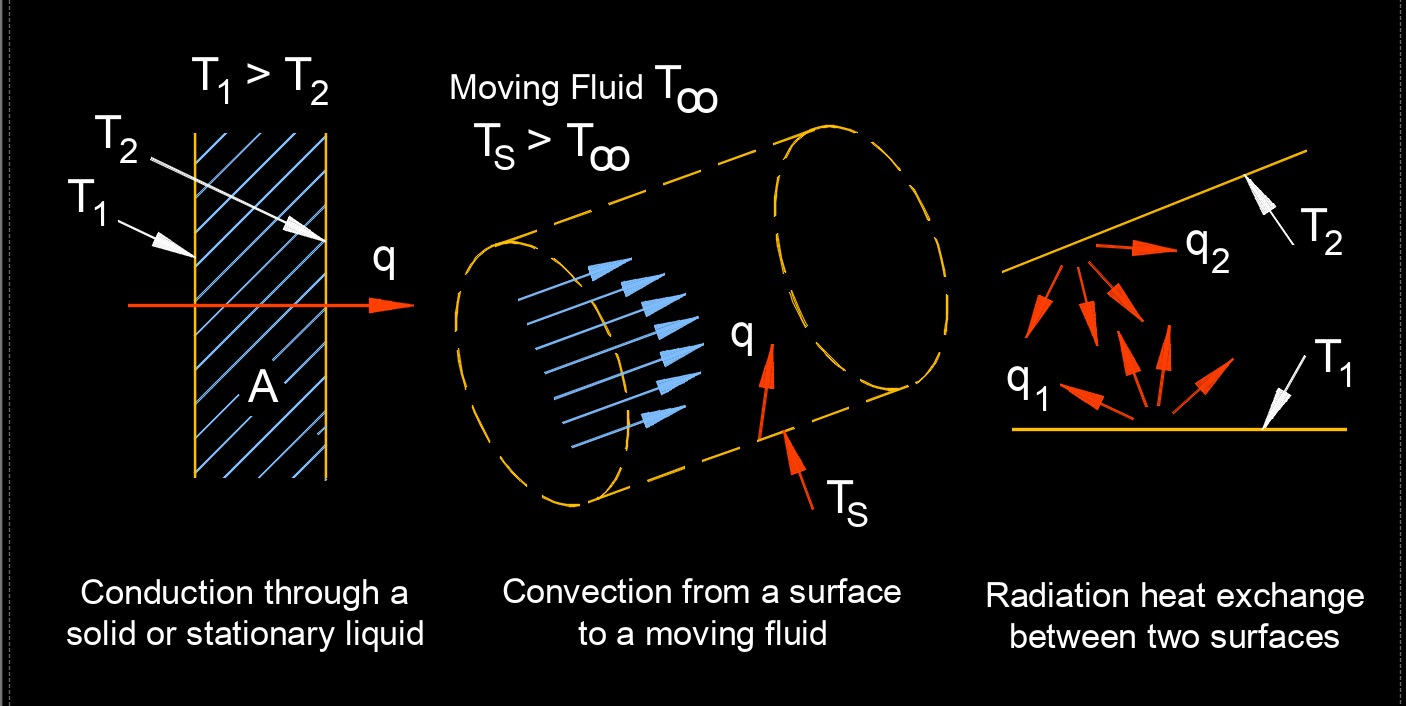
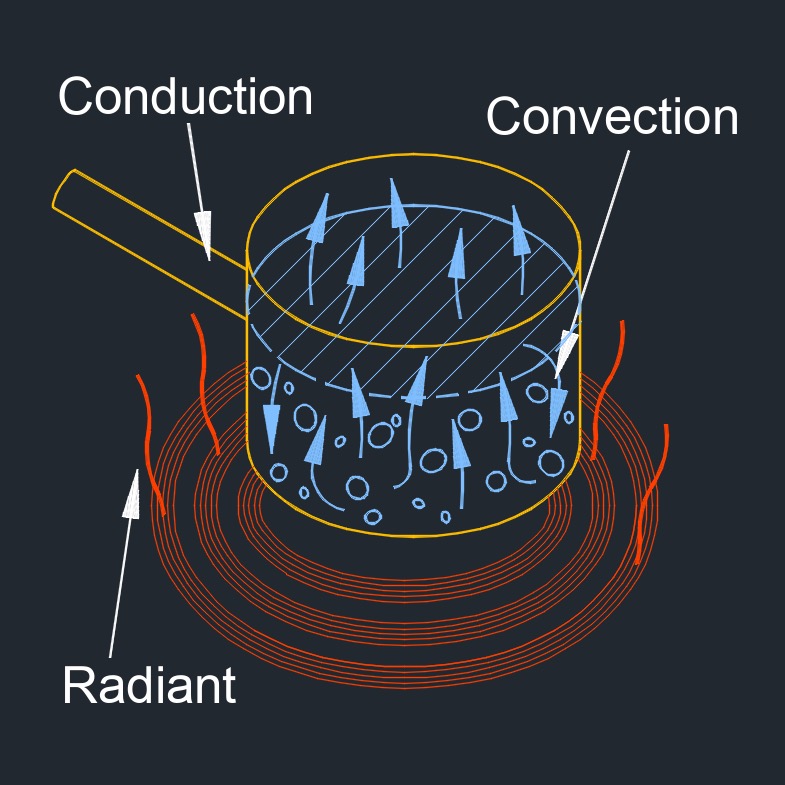
This transfer of thermal energy can occur through three modes of heat transfer: conduction, convection, and radiation. Heat transfer is an important concept in many fields, including engineering, physics, and thermodynamics. In practical scenarios, heat transfer often involves a combination of these three modes. For example, the heating of a room may involve conduction through the walls, convection of air within the room, and radiation from a heating element.
